
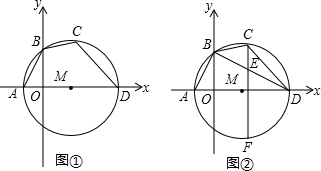
分析 (1)如图1中,连接BD.由△AOB∽△BOD,可得$\frac{OA}{OB}$=$\frac{OB}{OD}$,求出OD即可解决问题;
(2)如图1中,连接BD、AC、BM交AC于K.由△BOM≌△AKM,推出OM=MK=3,KB=2,AK=BO=CK=4,由AD是直径,推出∠ACD=90°,推出CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,根据S四边形ABCD=S△ABC+S△ACD计算即可;
(3)如图3中,连接DF、AC、作CH⊥BD于H.由△CBH∽△DAC,推出$\frac{BC}{AD}$=$\frac{BH}{AC}$=$\frac{CH}{CD}$,可得$\frac{2\sqrt{5}}{10}$=$\frac{BH}{8}$=$\frac{CH}{6}$,推出CH=$\frac{6\sqrt{5}}{5}$,BH=$\frac{8\sqrt{5}}{5}$,由BC=BE=2$\sqrt{5}$,推出HE=BE-BH=$\frac{2\sqrt{5}}{5}$,在Rt△CHE中,EC=$\sqrt{C{H}^{2}+H{E}^{2}}$=2$\sqrt{2}$,由△CBE∽△DFE,可得$\frac{EC}{DE}$=$\frac{BE}{EF}$,求出EF即可解决问题;
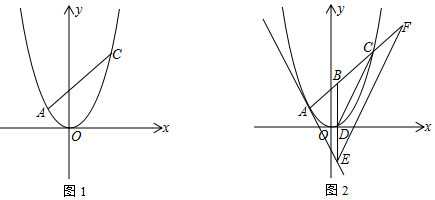
解答 解:(1)如图1中,连接BD.
∵AD时直径,
∴∠ABD=90°,
∵∠ABO+∠DBO=90°,∠DBO+∠BDO=90°,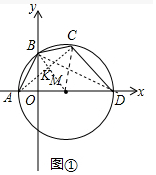
∴∠ABO=∠BDO,∵∠AOB=∠DOB=90°,
∴△AOB∽△BOD,
∴$\frac{OA}{OB}$=$\frac{OB}{OD}$,
∵A(0,-2),B(0,4),
∴OA=2,OB=4,
∴OD=8,
∴AD=10,OM=3,
∴M(3,0).
(2)如图1中,连接BD、AC、BM交AC于K.
∵AB=BC,
∴$\widehat{AB}$=$\widehat{BC}$,
∴MB⊥AC,
∵∠BOM=∠AKM=90°∠BMO=∠AMK,MA=MB,
∴△BOM≌△AKM,
∴OM=MK=3,KB=2,AK=BO=CK=4,
∵AD是直径,
∴∠ACD=90°,
∴CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$•AC•BK+$\frac{1}{2}$•AC•CD=$\frac{1}{2}$×8×2+$\frac{1}{2}$×6×8=32.
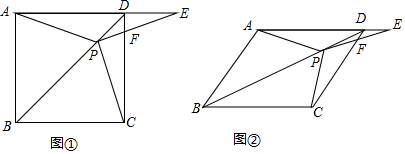
(3)如图3中,连接DF、AC、作CH⊥BD于H.
∵∠CBH=∠CAD,∠CHB=∠ACD=90°,
∴△CBH∽△DAC,
∴$\frac{BC}{AD}$=$\frac{BH}{AC}$=$\frac{CH}{CD}$,
∴$\frac{2\sqrt{5}}{10}$=$\frac{BH}{8}$=$\frac{CH}{6}$,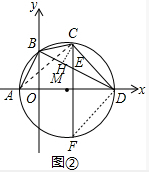
∴CH=$\frac{6\sqrt{5}}{5}$,BH=$\frac{8\sqrt{5}}{5}$,
∵BC=BE=2$\sqrt{5}$,
∴HE=BE-BH=$\frac{2\sqrt{5}}{5}$,
在Rt△CHE中,EC=$\sqrt{C{H}^{2}+H{E}^{2}}$=2$\sqrt{2}$,
∵∠CBE=∠F,∠BCE=∠EDF,
∴△CBE∽△DFE,
∴$\frac{EC}{DE}$=$\frac{BE}{EF}$,
∴$\frac{2\sqrt{2}}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{EF}$,
∴EF=5$\sqrt{2}$,
∴CF=CE+EF=2$\sqrt{2}$+5$\sqrt{2}$=7$\sqrt{2}$.
点评 本题考查圆综合题、相似三角形的判定和性质、勾股定理、垂径定理、直径的性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
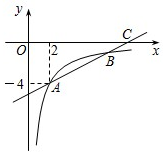 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
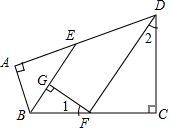 如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com