
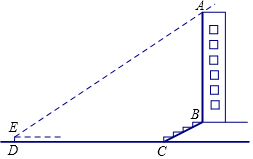
 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)分析 延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
解答  解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,$\frac{BF}{CF}$=i=1:$\sqrt{3}$,
∴设BF=k,则CF=$\sqrt{3}k$,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=$6\sqrt{3}$.
∵DF=DC+CF,
∴DF=40+6$\sqrt{3}$.
∵在Rt△AEH中,tan∠AEH=$\frac{AH}{EH}$,
∴AH=tan37°×(40+6$\sqrt{3}$)≈37.785(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=37.785-4.5≈33.3.
答:大楼AB的高度约为33.3米.
点评 本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow a-2\overrightarrow b$ | B. | $\frac{5}{2}\overrightarrow a-\overrightarrow b$ | C. | $\overrightarrow a-\frac{2}{3}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
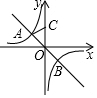 如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )
如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com