
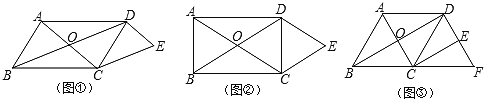
ЎѕМвДїЎї(1)·ўПЦОКМв:ИзНјўЩЖЅРРЛД±ЯРОABЎўCDµД¶ФЅЗПЯПаЅ»УЪµгO,DEЎОAC,CEЎОBDЈ¬їЙЦЄ:ЛД±ЯРОOCEDКЗКІГґРО(І»РиТЄЦ¤Гч).
(2)Аа±ИМЅѕї:ИзНјўЪѕШРОABCDµД¶ФЅЗПЯПаЅ»УЪµгO,DEЎОAC,CEЎОBDЈ¬ЛД±ЯРОOCEDКЗКІГґРО,ЗлЛµГчАнУЙЈ»
(3)НШХ№У¦УГ:ИзНјўЫ,БвРОABCDµД¶ФЅЗПЯПаЅ»УЪµгO,ЎПABC=60Ўг,BC=4,DEЎОACЅ»BCµДСУі¤ПЯУЪµгF,CEЎОBDЗуЛД±ЯРОABFDµДЦЬі¤.
Ўѕґр°ёЎї(1)ЖЅРРЛД±ЯРОЈ»ЈЁ2Ј©БвРОЈ¬Ц¤ГчјыЅвОцЈ»ЈЁ3Ј©20.
ЎѕЅвОцЎї
ЈЁ1Ј©АыУГБЅЧй¶Ф±ЯЖЅРРµДЛД±ЯРОКЗЖЅРРЛД±ЯРОЈ»
ЈЁ2Ј©ПИЕР¶ПіцЛД±ЯРОOCEDКЗЖЅРРЛД±ЯРОЈ¬ФЩУГѕШРОµДРФЦКјґїЙµГіцЅбВЫЈ»
ЈЁ3Ј©ПИЕР¶ПіцИэЅЗРОCDFКЗµИ±ЯИэЅЗРОЈ¬јґїЙµГіцЅбВЫЈ®
ЈЁ1Ј©ЎЯDEЎОACЈ¬CEЎОBD
ЎаЛД±ЯРОOCEDКЗЖЅРРЛД±ЯРОЈ¬
№Кґр°ёОЄЈєЖЅРРЛД±ЯРОЈ»
ЈЁ2Ј©ЛД±ЯРОOCEDКЗБвРОЈ¬
Ц¤ГчЈєЎЯDEЎОACЈ¬CEЎОBDЈ¬
ЎаЛД±ЯРОOCEDКЗЖЅРРЛД±ЯРОЈ¬
ЎЯЛД±ЯРОABCDКЗѕШРОЈ¬
ЎаOC=ODЈ¬
ЎаOCEDКЗБвРОЈ¬
№Кґр°ёОЄЈєБвРОЈ®
ЈЁ3Ј©ЎЯADЎОBCЈ¬DEЎОACЈ¬
ЎаЛД±ЯРОACFDКЗЖЅРРЛД±ЯРОЈ¬
ЎЯЛД±ЯРОABCDКЗБвРОЈ¬ЎПABC=60ЎгЈ¬BC=4Ј¬
ЎаAD=BC=AB=DC=4Ј¬ЎПDCF=60ЎгЈ¬
ЎаЎчDCFКЗµИ±ЯИэЅЗРОЈ¬
ЎаCF=DF=CD=4Ј¬
ЎаЛД±ЯРОABFDµДЦЬі¤ОЄAB+BC+CF+DF+AD=4ЎБ5=20Ј®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЯєюі¤ЅґуЗЕКЗЦР№ъїз¶ИЧоґуµД№«В·єНМъВ·БЅУГЗЕБєЈ¬ґуЗЕІЙУГµНЛюР±АЗЕЗЕРНЈЁИзјЧНјЈ©Ј¬НјТТКЗґУНјјЧТэЙкіцµДЖЅГжНјЈ¬јЩЙиДгХѕФЪЗЕЙПІвµГАЛчABУлЛ®ЖЅЗЕГжµДјРЅЗКЗ30ЎгЈ¬АЛчCDУлЛ®ЖЅЗЕГжµДјРЅЗКЗ60ЎгЈ¬БЅАЛч¶Ґ¶ЛµДѕаАлBCОЄ2ГЧЈ¬БЅАЛчµЧ¶ЛѕаАлADОЄ20ГЧЈ¬ЗлЗуіцБўЦщBHµДі¤Ј®ЈЁЅб№ыѕ«И·µЅ0.1ГЧЈ¬ ![]() ЎЦ1.732Ј©
ЎЦ1.732Ј©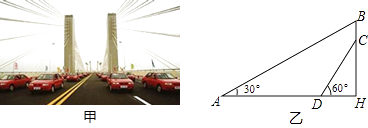
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЅ«Т»ё±ИэЅЗ°еИзНј°Ъ·ЕЈ¬ЎПOAB=ЎПOCD=90ЎгЈ¬ЎПAOB=60ЎгЈ¬ЎПCOD=45ЎгЈ¬OMЖЅ·ЦЎПAODЈ¬ONЖЅ·ЦЎПCOBЈ¬ФтЎПMONµД¶ИКэОЄЈЁ Ј©
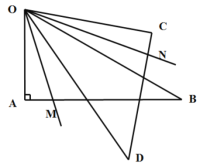
A.60ЎгB.45ЎгC.65.5ЎгD.52.5Ўг
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЈЁ1Ј©ЖґТ»ЖґЈ¬»Т»»ЈєЗлДгУГ4ёці¤ОЄaЈ¬їнОЄbµДѕШРОЖґіЙТ»ёцґуХэ·ЅРОЈ¬ІўЗТХэЦРјдБфПВТ»ёц¶ґЈ¬Хвёц¶ґЗЎєГКЗТ»ёцРЎХэ·ЅРОЎЈ

ЈЁ2Ј©УГІ»Н¬·Ѕ·ЁјЖЛгЦРјдµДРЎХэ·ЅРОµДГж»эЈ¬ґПГчµДДгДЬ·ўПЦКІГґЈї
ЈЁ3Ј©µ±ЖґіЙµДХвёцґуХэ·ЅРО±Яі¤±ИЦРјдРЎХэ·ЅРО±Яі¤¶а3cmК±Ј¬ЛьµДГж»эѕН¶а24cm2Ј¬ЗуЦРјдРЎХэ·ЅРОµД±Яі¤ЎЈ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЦ±ПЯlЈєy=mx©Ѓm+1ЈЁmОЄіЈКэЈ¬ЗТmЎЩ0Ј©УлЧш±кЦбЅ»УЪAЎўBБЅµгЈ¬ИфЎчAOBЈЁOКЗФµгЈ©µДГж»эЗЎОЄ2Ј¬Фт·ыєПТЄЗуµДЦ±ПЯlУРЈЁ Ј©
A.1Мх
B.2Мх
C.3Мх
D.4Мх
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪХэ·ЅРОABCDЦРЈ¬µгPКЗABµДЦРµгЈ¬![]() µДСУі¤ПЯУЪµгEЈ¬Б¬ЅУAEЈ¬№эµгAЧч
µДСУі¤ПЯУЪµгEЈ¬Б¬ЅУAEЈ¬№эµгAЧч![]() Ѕ»DPУЪµгFЈ¬Б¬ЅУBFЎў
Ѕ»DPУЪµгFЈ¬Б¬ЅУBFЎў![]() ПВБРЅбВЫЦРЈє
ПВБРЅбВЫЦРЈє![]() ЎХ
ЎХ![]() Ј»
Ј»![]() Ј»
Ј»![]() КЗµИ±ЯИэЅЗРОЈ»
КЗµИ±ЯИэЅЗРОЈ»![]() Ј»
Ј»![]() ЖдЦРХэИ·µДКЗ
ЖдЦРХэИ·µДКЗ![]() ЎЎЎЎ
ЎЎЎЎ![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЦ±ЅЗМЭРОABCDЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®
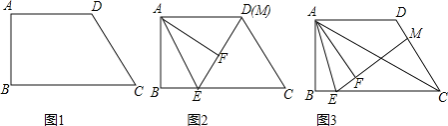
ЈЁ1Ј©ИзНј1Ј¬Б¬ЅУACЈ¬ЗуЦ¤ЈєCAКЗ![]() µДЖЅ·ЦПЯЈ»
µДЖЅ·ЦПЯЈ»
ЈЁ2Ј©ПЯ¶ОBCЙПТ»µгEЈ¬Ѕ«![]() СШAE·ХЫЈ¬µгBВдµЅµгFґ¦Ј¬ЙдПЯEFУлПЯ¶ОCDЅ»УЪµгMЈ®
СШAE·ХЫЈ¬µгBВдµЅµгFґ¦Ј¬ЙдПЯEFУлПЯ¶ОCDЅ»УЪµгMЈ®
ўЩИзНј2Ј¬µ±µгMУлµгDЦШєПК±Ј¬ЗуЦ¤Јє![]() Ј»
Ј»
ўЪИзНј3Ј¬µ±µгMІ»УлµгDЦШєПК±Ј¬ЗуЦ¤Јє![]() Ј®
Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїјЖЛг»т»ЇјтЈє
ЈЁ1Ј©2©Ѓ1+![]()
ЈЁ2Ј©2x2yЈЁ©Ѓ3xyЈ©ЎВЈЁxyЈ©2
ЈЁ3Ј©ЈЁ©Ѓ2aЈ©ЈЁ3a2©Ѓa+3Ј©
ЈЁ4Ј©ЈЁx+3Ј©ЈЁx+4Ј©©ЃЈЁx©Ѓ1Ј©2
ЈЁ5Ј©[2a3x2ЈЁa©Ѓ2xЈ©©Ѓ![]() a2x2]ЎВЈЁ©ЃaxЈ©2
a2x2]ЎВЈЁ©ЃaxЈ©2
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ОЄБЛІвіцДіЛюCDµДёЯ¶ИЈ¬ФЪЛюЗ°µДЖЅµШЙПСЎФсТ»µгAЈ¬УГІвЅЗТЗІвµГЛю¶ҐDµДСцЅЗОЄ30ЎгЈ¬ФЪAЎўCЦ®јдСЎФсТ»µгBЈЁAЎўBЎўCИэµгФЪН¬Т»Ц±ПЯЙПЈ©Ј®УГІвЅЗТЗІвµГЛю¶ҐDµДСцЅЗОЄ75ЎгЈ¬ЗТABјдµДѕаАлОЄ40mЈ®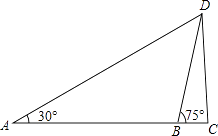
ЈЁ1Ј©ЗуµгBµЅADµДѕаАлЈ»
ЈЁ2Ј©ЗуЛюёЯCDЈЁЅб№ыУГёщєЕ±нКѕЈ©Ј®
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com