
 ),两个不全等的等腰直角三角形
),两个不全等的等腰直角三角形 和
和 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点 .
.
 )中的
)中的 绕点
绕点 顺时针旋转
顺时针旋转 角,在图(
角,在图( )中作出旋转后的
)中作出旋转后的 (保留作图痕迹,不写作法,不证明).
(保留作图痕迹,不写作法,不证明). )中,你发现线段
)中,你发现线段 ,
, 的数量关系是 ,直线
的数量关系是 ,直线 ,
, 相交成 度角.
相交成 度角. )中的
)中的 绕点
绕点 顺时针旋转一个锐角,得到图(
顺时针旋转一个锐角,得到图( ),这时(2)中的两个结论是否成立?作出判断并说明理由.若
),这时(2)中的两个结论是否成立?作出判断并说明理由.若 绕点
绕点 继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.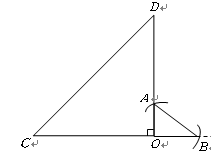 (2)
(2) ;
; (3)成立,理由见解析
(3)成立,理由见解析 )(
)( 字母位置互换扣1分,无弧扣1分,不连结
字母位置互换扣1分,无弧扣1分,不连结 扣1分,扣完为止) 3分
扣1分,扣完为止) 3分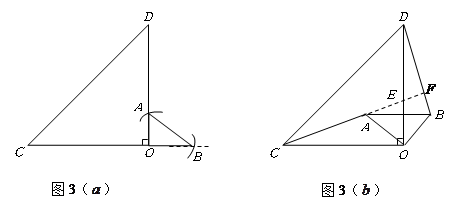
 ;
;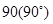 (每空1分)·················· 5分
(每空1分)·················· 5分 )
)

 (或由旋转得
(或由旋转得 )············· 7分
)············· 7分
 ·············· 8分
·············· 8分 ································ 9分
································ 9分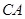 交
交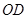 于
于 ,交
,交 于
于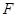 (下面的证法较多)
(下面的证法较多) ,
,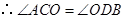 ·················· 10分
·················· 10分
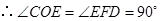
 ······· 11分
······· 11分
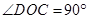


科目:初中数学 来源:不详 题型:解答题
 ∠ABC ,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
∠ABC ,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明. ∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?请直接写出猜想,不需证明.
∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?请直接写出猜想,不需证明.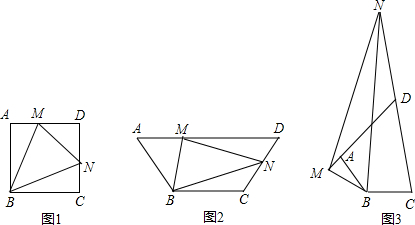
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 重合,画出平移后的三角形.
重合,画出平移后的三角形. 逆时针旋转
逆时针旋转 ,画出旋转后的图形.
,画出旋转后的图形.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 (个)小正方形.
(个)小正方形. (个)小正方形.
(个)小正方形.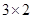 个小正方形,从而分割成
个小正方形,从而分割成 (个)小正方形.
(个)小正方形.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (0°<
(0°< <180°),得到△A′B′C.
<180°),得到△A′B′C. ,连接EP, 当
,连接EP, 当 = °时,EP长度最大,最大值为 .
= °时,EP长度最大,最大值为 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.30° | B.60° | C.90° | D.180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com