
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于点A,B两点,点A在点B的左侧,点M为AB的中点,PQ![]() x轴交抛物线于点P,Q,点P在点Q的左侧,点Q在第一象限,以PQ,PM为邻边作PMNQ.设点P的横坐标为m.
x轴交抛物线于点P,Q,点P在点Q的左侧,点Q在第一象限,以PQ,PM为邻边作PMNQ.设点P的横坐标为m.

(1)当m=0时,求PMNO的周长;
(2)连结MQ,若MQ⊥QN时,求m的值.
【答案】(1)4+2![]() ;(2)
;(2)![]()
【解析】
(1)根据题意求得P(0,3),Q(2,3),则PQ=2,由勾股定理得PM长,则PMNO的周长可求出;
(2)由题意知△PQM为等腰直角三角形,P(m,﹣m2+2m+3),有Q(2﹣m,﹣m2+2m+3),则PQ=2﹣2m,可得关于m的方程,解方程可求出m的值.
解:(1)令x=0得,y=3
∴P(0,3),
∵抛物线的对称轴为:直线x=﹣![]() ,
,
∴M(1,0),
∵PQ∥x轴,
∴Q(2,3),即得PQ=2,
PM=![]() =
=![]() ,
,
∵PMNQ为平行四边形,
∴QN=PM=![]() ,MN=PQ=2,
,MN=PQ=2,
∴PMNQ的周长为:QN+PM+MN+PQ=4+2![]() .
.
(2)如图,连接MQ,

∵PMNQ为平行四边形,
∴PM∥QN,
∵MQ⊥QN,
∴MQ⊥PM,
∵P,Q关于对称轴对称,
∴MP=MQ,
∴△PQM为等腰直角三角形,
∴![]() ,
,
∵P(m,﹣m2+2m+3),
∴Q(2﹣m,﹣m2+2m+3),
∴PQ=2﹣2m,
∴﹣![]() ,
,
解得![]() ,m2=
,m2=![]() ,
,
∵P在Q左侧,
∴m=![]() .
.


科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于![]() 左右,求n的值;
左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,某水厂规定:某单元居民如果一个月的用水量不超过![]() 吨,那么这个月该单元居民只交10元水费.如果超过
吨,那么这个月该单元居民只交10元水费.如果超过![]() 吨,则这个月除了仍要交10元水费外,超过那部分按每吨
吨,则这个月除了仍要交10元水费外,超过那部分按每吨![]() 元交费.
元交费.
(1)该单元居民8月份用水80吨,超过了“规定的![]() 吨”,则超过部分应交水费 (80-x)
吨”,则超过部分应交水费 (80-x)
元(用含x的式子表示).
(2)下表是该单元居民9月、10月的用水情况和交费情况:
月份 | 用水量(吨) | 交费总数(元) |
9月份 | 85 | 25 |
10月份 | 50 | 10 |
根据上表数据,求该x吨是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A,B分别在x轴负半轴,y轴负半轴上,AD交y轴于点F,E为CD的中点.若OB=1,BD=2EF时,反比例函数y=![]() 的图象经过D,E两点,则k的值为_____.
的图象经过D,E两点,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=x和![]() 的图象分别为直线l1、l2,过点A1(1,
的图象分别为直线l1、l2,过点A1(1,![]() )作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……依次进行下去,则点A2019的横坐标为( )
)作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……依次进行下去,则点A2019的横坐标为( )
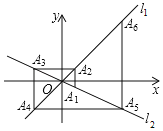
A.21008B.﹣21008C.﹣21009D.21006
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是对角线BD上一动点.
(1)如图1,当CE⊥BD时,求DE的长;
(2)如图2,作EM⊥EN分别交边BC于M,交边CD于N,连MN.
①若![]() ,求tan∠ENM;
,求tan∠ENM;
②若E运动到矩形中心O,连CO.当CO将△OMN分成两部分面积比为1:2时,直接写出CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
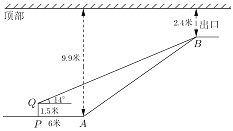
【题目】地铁10号线某站点出口横截面平面图如图所示,电梯![]() 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点![]() 端6米的
端6米的![]() 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端![]() 处的仰角为14°,求电梯
处的仰角为14°,求电梯![]() 的坡度与长度.(参考数据:
的坡度与长度.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
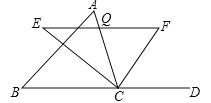
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com