
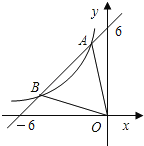
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解.
的解.
【答案】(1) ![]() ;(2) 6;(3) -4<x<-2.
;(2) 6;(3) -4<x<-2.
【解析】试题分析:(1)根据待定系数法就可以求出函数的解析式;
(2)求△AOB的面积就是求A,B两点的坐标,将一次函数与反比例函数的解析式组成方程即可求得;
(3)观察图象即可求得一次函数比反比例函数大的区间.
试题解析:(1)设一次函数解析式为y=kx+b,
∵一次函数与坐标轴的交点为(-6,0),(0,6),
∴![]() 解得:
解得: ![]() ,
,
∴一次函数关系式为:y=x+6,
∴B(-4,2),
∴反比例函数关系式为: ![]() ;
;
(2)∵点A与点B是反比例函数与一次函数的交点,
∴![]() ,
,
解得:x=-2或x=-4,
∴A(-2,4),
∴S△AOB=6×6÷2-6×2=6;
(3)-4<x<-2.
考点: 反比例函数与一次函数的交点问题.


科目:初中数学 来源: 题型:
【题目】某频数分布直方图中,共有A、B、C、D、E五个小组,频数分布为10、15、25、35、10,则直方图中,长方形高的比为( )
A.2﹕3﹕5﹕7﹕2
B.1﹕3﹕4﹕5﹕1
C.2﹕3﹕5﹕6﹕2
D.2﹕4﹕5﹕4﹕2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起.
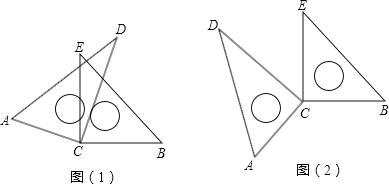
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
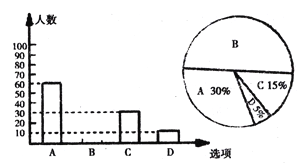
【题目】为了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”共有4个选题.
A.1.5小时以上 B.1~1.5小时 C.0.5~1小时 D.0.5小时以下
请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)将条形统计图选项B补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com