
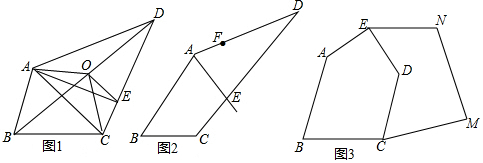
分析 (1)如图1中,作AH⊥BC于H.由S△ABD=$\frac{1}{2}$•BD•AH,S△ADC=$\frac{1}{2}$•DC•AH,因为BD=CD,所以S△ABD=S△ADC,再判断出S四边形ABCO=$\frac{1}{2}$S四边形ABCD,进而判断出S△AOE=S△COE,推出S△AOF=S△CEF,即可推出直线AE平分四边形ABCD的面积;
(2)连接EF,过A作EF的平行线交CD于点G,连接FG,则GF为一条“好线”.由AG∥EF,推出S△AGE=S△AFG.设AE与FG的交点是O.则S△AOF=S△GOE,又AE为一条“好线”,所以GF为一条“好线”,
(3)连接CE,过点D作DF∥EC交CM于F,连接EF,即EF为所修的直路,利用夹在平行线间的距离处处相等得出
DG=FH,即可得出S△CDE=S△CEF,结论得证.
解答 解:(1)∵点O是BD的中点,
∴S△AOB=S△AOD,S△BOC=S△DOC,
∴S△AOB+S△BOC=S△AOD+S△DOC=$\frac{1}{2}$S四边形ABCD,
∴S四边形ABCO=$\frac{1}{2}$S四边形ABCD.
∴折线AOC能平分四边形ABCD的面积,
设AE交OC于F.
∵OE∥AC,
∴S△AOE=S△COE,
∴S△AOF=S△CEF,
∵折线AOC能平分四边形ABCD的面积,
∴直线AE平分四边形ABCD的面积,即AE是四边形ABCD的一条“好线”.
(2)连接EF,过A作EF的平行线交CD于点G,连接FG,则GF为一条“好线”.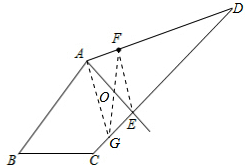
∵AG∥EF,
∴S△AGE=S△AFG.
设AE与FG的交点是O.则S△AOF=S△GOE,
又AE为一条“好线”,所以GF为一条“好线”.
(3)如图3,
连接CE,过点D作DF∥EC交CM于F,连接EF,即EF为所修的直路,
理由:过点D作DG⊥CE于G,过点F作FH⊥EC于H,
∵DF∥EC,∴DG=FH(夹在平行线间的距离处处相等),
∵S△CDE=$\frac{1}{2}$EC×DG,S△CEF=$\frac{1}{2}$EC×FH,
∴S△CDE=S△CEF,
∴S四边形ABCDE=S四边形ABCE+S△CDE=S四边形ABCE+S△CEF=S五边形ABCFE.
即:直路左边的土地面积与原来一样多.
点评 本题考查四边形综合题、三角形中线的性质、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,理解同底等高的三角形面积相等,属于中考创新题目.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:填空题
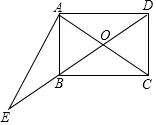 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 应试者 | 测试成绩 | ||
| 创新能力 | 计算机能力 | 公关能力 | |
| 甲 | 72 | 50 | 88 |
| 乙 | 85 | 74 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
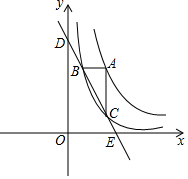 如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数y=$\frac{4}{x}$(x>0)图象上运动时,
如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数y=$\frac{4}{x}$(x>0)图象上运动时,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
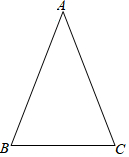 如图,在△ABC中,AB=AC,作AB的垂直平分线DE分别交AB,AC于点D,E,连接BE,则:
如图,在△ABC中,AB=AC,作AB的垂直平分线DE分别交AB,AC于点D,E,连接BE,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
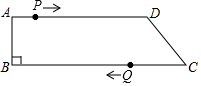 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在平面直角坐标系xOy中,O为坐标原点,点A,B分别在x轴上(点A在原点左侧,点B在原点右侧),OB=4OA,经过点A,B的抛物线交y轴于点C(0,2),且∠ACB=90°.
如图,已知在平面直角坐标系xOy中,O为坐标原点,点A,B分别在x轴上(点A在原点左侧,点B在原点右侧),OB=4OA,经过点A,B的抛物线交y轴于点C(0,2),且∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com