
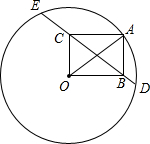
 如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是
如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是 解:如图,设DE的中点为M,连接OM,则OM⊥DE.
解:如图,设DE的中点为M,连接OM,则OM⊥DE.| OA2-AB2 |
| 202-122 |
| OB•OC |
| BC |
| 16×12 |
| 20 |
| 48 |
| 5 |
| OC2-OM2 |
122-(
|
| 36 |
| 5 |
| 36 |
| 5 |
| 64 |
| 5 |
| 64 |
| 5 |
| 36 |
| 5 |
| 28 |
| 5 |
| 28 |
| 5 |


科目:初中数学 来源: 题型:
 正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°
正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 规作图确定医院M的位置.(不要求写出作法、证明,但要保留作图痕迹,请务必用铅笔作图).
规作图确定医院M的位置.(不要求写出作法、证明,但要保留作图痕迹,请务必用铅笔作图).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC内接于⊙O,AD是BC边上的高,AO的延长线交⊙O于点E.已知AB=
如图,△ABC内接于⊙O,AD是BC边上的高,AO的延长线交⊙O于点E.已知AB=| 6 |
| 3 |
A、3
| ||
B、2
| ||
C、3
| ||
D、2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| b |
| a |
| c |
| a |
| 1 |
| (a2-2)(b2-2) |
| 1 |
| (a3-2)(b3-2) |
| 1 |
| (an-2)(bn-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠C=∠EFB.
如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠C=∠EFB.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com