
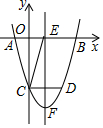
 ��ͼ��������y=x2+mx+n������A��-1��0������x�����һ��������B��B��A���Ҳࣩ����y�ύ�ڵ�C�������ߵĶԳ���EF��x���ڵ�E����C����EF�ĶԳƵ���D���Ե�B��C��D��EΪ�������ı��Σ����Ե�B��C��D��EΪ������ı��ε����ΪS��
��ͼ��������y=x2+mx+n������A��-1��0������x�����һ��������B��B��A���Ҳࣩ����y�ύ�ڵ�C�������ߵĶԳ���EF��x���ڵ�E����C����EF�ĶԳƵ���D���Ե�B��C��D��EΪ�������ı��Σ����Ե�B��C��D��EΪ������ı��ε����ΪS������ ��1���ѵ�A��-1��0������������y=x2+mx+n�������ú�m�Ĵ���ʽ��ʾn��
��2����������ȵĵ���ڶԳ���Գƣ��ɵô�
��3���������ε������ʽ���ɵô𰸣�
��4������ƽ���ı��ε����ʣ��ɵù���m�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1����������y=x2+mx+n������A��-1��0����
��1-m+n=0��
��n=m-1��
�ʴ�Ϊ��m-1��
��2��������y=x2+mx+m-1�ĶԳ�����x=-$\frac{m}{2}$��
��BE=AE=-$\frac{m}{2}$+1��
��3��0��m��2ʱ���ı���BECD�����Σ�BE=-$\frac{m}{2}$+1��CD=m��OC=m-1��
S=$\frac{��BE+CD��•OC}{2}$=$\frac{��-\frac{m}{2}+1+m��•��m-1��}{2}$
��S=$\frac{{m}^{2}+m-2}{4}$��
��m��0ʱ���ı���BECD�����Σ�BE=-$\frac{m}{2}$+1��CD=-m��OC=1-m��
S=$\frac{��BE+CD��•OC}{2}$=$\frac{��-\frac{m}{2}+1-m����1-m��}{2}$
��S=$\frac{3{m}^{2}-4m+1}{4}$��
��4����3���ٵ�m��0ʱ����ͼ1��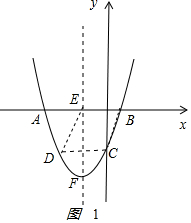
��������y=x2+mx+m-1�ĶԳ�����x=-$\frac{m}{2}$��
��CD=m��BE=AE=-$\frac{m}{2}$+1��
���ı���ACDE��ƽ���ı��Σ�
��m=-$\frac{m}{2}$+1��
��m=$\frac{2}{3}$��
�ڵ�-2��m��0ʱ����ͼ2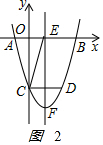 ��
��
CD=-m��BE=AE=-$\frac{m}{2}$+1��
���ı���ADCE��ƽ���ı��Σ�
��-m=-$\frac{m}{2}$+1��
��m=-2��
���� ���⿼���˶��κ����ۺ��⣬�⣨1���Ĺؼ������ô���ϵ�������⣨2���Ĺؼ����������������߶Գ��ṫʽ���е����깫ʽ���⣨3���Ĺؼ����������ε������ʽ��Ҫ�������ۣ��Է���©���⣨4���Ĺؼ�������ƽ���ı��ε����ʵó�����m�ķ��̣�Ҫ�������ۣ��Է���©��


 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ھ���OABCֽƬ�У�OA=7��OC=5��DΪBC���϶��㣬����OCD��OD�۵�������C�Ķ�Ӧ������ֱ��l��y=-x+7��ʱ����Ϊ��E��F������C�Ķ�Ӧ�����ڱ�OA��ʱ����Ϊ��G��
��ͼ���ھ���OABCֽƬ�У�OA=7��OC=5��DΪBC���϶��㣬����OCD��OD�۵�������C�Ķ�Ӧ������ֱ��l��y=-x+7��ʱ����Ϊ��E��F������C�Ķ�Ӧ�����ڱ�OA��ʱ����Ϊ��G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
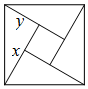 ��ͼ����4��ȫ�ȵ�ֱ����������Ƕ���ɵ�������ͼ������֪�������ε����Ϊ49��С�����ε����Ϊ4������x��y��ʾֱ�������ε�����ֱ�DZߣ�x��y������۲�ͼ����ָ�����й�ϵʽ����ȷ���ǣ�������
��ͼ����4��ȫ�ȵ�ֱ����������Ƕ���ɵ�������ͼ������֪�������ε����Ϊ49��С�����ε����Ϊ4������x��y��ʾֱ�������ε�����ֱ�DZߣ�x��y������۲�ͼ����ָ�����й�ϵʽ����ȷ���ǣ�������| A�� | x2+y2=49 | B�� | x-y=2 | C�� | 2xy+4=49 | D�� | x+y=13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com