
�ס������˲μ����ʵ��������ѡ��ɨ�����������͡��μ������顱����һ���ô����ͬʱѡ�μ������顱�ĸ���Ϊ�� ��
A. 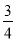 B.
B. 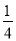 C.
C. 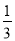 D.
D. 

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��֪��AOB��30�㣬���ԡ�AOB�Ķ���O������OC������AOC����AOB��4��3����ô��BOC�� ( )
A. 10�� B. 40�� C. 45�� D. 70���10��
D ������������������ߡ�AOB=30�㣬��AOC����AOB=4��3�� ���AOC=40�� ��OC��OA�����ʱ����BOC=��AOC+��AOB=40��+30��=70�㣻 ��OC��OB����࣬��BOC=��AOC-��AOB=40��-30��=10�㣮 ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݴ���2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ����֪ ��
�� 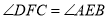 ��
��  ����֤��
����֤�� 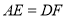 ��
��
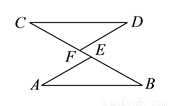
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪���κ���y=ax2+bx+4��ͼ����x�ύ�ڵ�B��-2��0������C��8��0������y�ύ�ڵ�A��
��1������κ���y=ax2+bx+4�ı���ʽ��
��2������AC��AB������N���߶�BC���˶��������B��C�غϣ�������N��NM��AC����AB�ڵ�M������AMN������ʱ����N������ꣻ
��3������OM���ڣ�2���Ľ����£���OM��AC��������ϵ��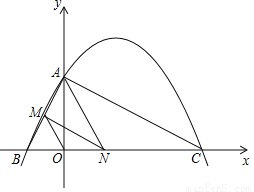
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ס�����յ·�Ƶײ���ľ���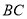 Ϊ
Ϊ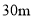 ��һ�����ϣ���С���ߵ���·���ҵײ�
��һ�����ϣ���С���ߵ���·���ҵײ�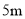 ��ʱ�������Լ�����Ӱ�������ýӴ�·���ҵĵײ�����֪С��������
��ʱ�������Լ�����Ӱ�������ýӴ�·���ҵĵײ�����֪С��������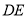 Ϊ
Ϊ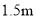 ����·�Ƽ�
����·�Ƽ�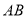 �ĸ߶ȣ�
�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ������
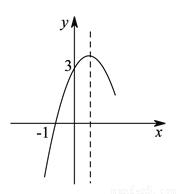
��֪���κ���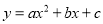 �IJ���ͼ����ͼ��ʾ���Գ���Ϊֱ��
�IJ���ͼ����ͼ��ʾ���Գ���Ϊֱ��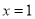 �������
�������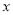 �ķ���
�ķ���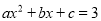 �Ľ�Ϊ__________��
�Ľ�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ������
��֪���ε�Բ�Ľ�Ϊ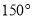 ������Ϊ
������Ϊ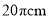 ����������εİ뾶Ϊ__________
����������εİ뾶Ϊ__________ 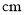 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������۴����2017-2018ѧ���һѧ����ĩ�������꼶��ѧ�Ծ����𰸣�WORD�棩 ���ͣ������
����:80��-45��17��=__________.
34��43�� ����������Ϊ1��=60��,����80��-45��17��=79��60��-45��17��=34��43��,�ʴ�Ϊ: 34��43��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����л�����2017-2018ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
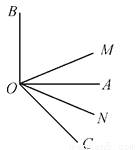
��ͼ����AOB��ֱ�ǣ�ON�ǡ�AOC��ƽ���ߣ�OM�ǡ�BOC��ƽ���ߣ�
(1)����AOC��40�㣬�����MON�Ĵ�С����д�����������ɣ�
(2)����AOC��50�㣬�����MON�Ĵ�С����д�����������ɣ�
(3)����ǡ�AOC=��ʱ�������MON�Ĵ�С����д������������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com