
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E。
(1)求证:DE=AB;
(2)以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,试求![]() 的长。
的长。

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=![]() ,∠GDE=∠BAF=30°,根据弧长公式求得求出即可.
,∠GDE=∠BAF=30°,根据弧长公式求得求出即可.
试题解析:(1)在△ABF和△DEA中,
∠AFB=∠DAE
∠B=∠DEA
AF=AD,
∴△ABF≌△DEA ∴DE=AB.
(2)∵BC=AD,AD=AF,
∴BC=AF.
∵BF=1,∠ABF=90°,
∴由勾股定理得:AB=![]()
∴∠BAF=30°.
∵△ABF≌△DEA,
∴∠GDE=∠BAF=30°,DE=AB=DG=![]()
∴ ![]() 的长为
的长为![]()


科目:初中数学 来源: 题型:
【题目】将连续奇数1,3,5,7,9,……排成如下的数表:
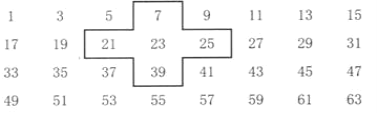
……………
(1)设中间的数为a,求这十字框中五个数之和(请用含字母a的代数式表示);
(2)将十字框上、下、左、右平移,可框住另外五个数,这五个数还有这种规律吗?
(3)十字框中的五个数的和能等于2015吗?若能,请求出这五个数;若不能,说明理由。那么2012呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离是时间的函数吗?如果是,写出函数的解析式,并画出函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数![]() .按要求完成下列各题.
.按要求完成下列各题.
(1)请把题中各数填入相应的集合中:
①整数集合:{ …}
②负数集合:{ …}
(2)把题中各数用数轴上的点表示出来,并用“<“连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①若![]() ,则
,则![]() ;②整数和分数统称为有理数;③绝对值等于它本身的整数是0;④
;②整数和分数统称为有理数;③绝对值等于它本身的整数是0;④![]() 是二次三项式;⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负数,其中判断正确的有( )
是二次三项式;⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负数,其中判断正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]() .
.
(2)如图,一次函数y=x+b与反比例函数![]() 在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若S△BCO=
在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若S△BCO= ![]() ,求一次函数和反比例函数的解析式.
,求一次函数和反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com