
【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2![]() ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.

【答案】(1)AF= ![]() (2)结论:AF=
(2)结论:AF= ![]() (3)4
(3)4![]() 或2
或2![]()
【解析】试题分析:(1)如图①中,只要证明△AEF是等腰直角三角形即可得到结论AF=![]() AE;
AE;
(2)如图②中,连接EF,DF交BC于K,先证明△EKF≌△EDA,再证明△AEF是等腰三角形即可;
(3)如图③中,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.
试题解析:(1)AF= ![]()
如图2,结论:AF= ![]()
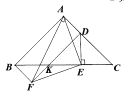
理由:连接EF,DF交BC于K,
∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DKE=∠ABC=45°
∴∠EKF=180°=∠DKE=135°,
∵∠ADE=180°-∠EDC=180°-45°=135°,∴∠EKF=∠ADE,
∵∠DKG=∠C,∴DK=DC,
∵DF=AB=AC,∴KF=AD,
在△EKF和△EDA中,
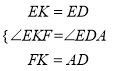
∴△EKF≌△EDA
∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,
∴AF=![]() AE
AE
(3)4![]() 或2
或2![]()


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,2),直线y= ![]() 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波轨道交通3号线于2014年12月23日开工建设,预计2020年全线开通,3号线全长32.83千米,32.83千米用科学记数法表示为( )
A.3.283×104米
B.32.83×104米
C.3.283×105米
D.3.283×103米
查看答案和解析>>
科目:初中数学 来源: 题型:
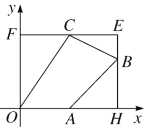
【题目】如图,四边形OABC各个顶点的坐标分别是O(0,0)、A(2,0)、B(4,2)、C(2,3),过点C与![]() 轴平行的直线EF与过点B与
轴平行的直线EF与过点B与![]() 轴平行的直线EH交于点E.
轴平行的直线EH交于点E.
求四边形OABC的面积;
在线段EH上是否存在点P,使四边形OAPC的面积为7?若不存在,说明理由,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com