
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
| 素质测试 | 测试成绩 | |||
| 李兵 | 张军 | 赵海 | 王洋 | |
| 计算机 | 70 | 80 | 75 | 70 |
| 商品知识 | 60 | 65 | 75 | 65 |
| 语言 | 80 | 75 | 70 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
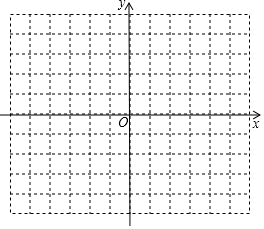 如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).
如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
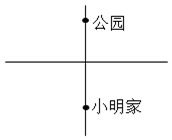 如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com