
【题目】在“元旦”期间,七(1)班小明,小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:

(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票省钱?请说明理由.
(3)正要购票时,小明发现七(2)班的小张等10名同学和他们的7名家长共17人也来购票,为了节省费用,经协商,他们决定一起购票,请你为他们设计最省钱的购票方案,并求出此时的费用.
【答案】(1)小明他们一共去了8个成人,4个学生(2)购买16张团体票省钱,详见解析(3)15个大人加上一个学生购买16张团体票,剩下的13名学生购买13张学生票,此时共需644元
【解析】
(1)设成人人数为x人,则学生人数为(12x)人,由题中所给的票价单可得出关于x的一元一次方程,解此方程即可得出成人与学生各有多少人数;
(2)已知购个人票的价钱,再算出购团体票的价钱,哪个更低哪个就更省钱;
(3)分三种情况讨论,再把价钱比较,即可得最省的购票方案.
解:(1)设小明他们一共去了![]() 个成人,则去了
个成人,则去了![]() 个学生,
个学生,
根据题意得:![]() ,
,
解得:![]() ,
,
∴![]()
答:小明他们一共去了8个成人,4个学生.
(2)![]() (元),
(元),
384元![]() 400元,
400元,
答:购买16张团体票省钱.
(3)①![]() (元)
(元)
②![]() (元),
(元),
③![]() (元)
(元)
答:15个大人加上一个学生购买16张团体票,剩下的13名学生购买13张学生票,此时共需644元.


科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+4x﹣3的“旋转函数”.小明是这样思考的:由函数y=﹣x2+4x﹣3可知,a1=﹣1,b1=4,c1=﹣3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.
(1)请参考小明的方法写出函数y=﹣x2+4x﹣3的“旋转函数”;
(2)若函数![]() 与y=x2﹣3nx+n互为“旋转函数”,求
与y=x2﹣3nx+n互为“旋转函数”,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式.并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多20%,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点开始沿一条东西方向的直线爬行,规定以出发点为原点,向东爬行的路程记为正数,向西爬行的路程记为负数,则蜗牛爬过的各段路程依次为+5,-3,+10,-8,-6,+12,-10.(单位:厘米)
(1)请判断蜗牛最后是否回到出发点?
(2)蜗牛离开出发点0最远时是多少厘米?
(3)在爬行过程中,若蜗牛每爬1厘米就奖励一粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决后面的问题.
材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707-1783)才发现指数与对数之间的联系.我们知道,n个相同的因数a相乘![]() 记为
记为![]() ,如
,如![]() ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为![]() ,即
,即![]() .
.
一般地,若![]() (
(![]() 且
且![]() ,
,![]() ),则n叫做以a为底b的对数,记为
),则n叫做以a为底b的对数,记为![]() ,即
,即![]() .如
.如![]() ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为![]() ,即
,即![]() .
.
(1)计算下列各对数的值:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)通过观察(1)中三数![]() 、
、![]() 、
、![]() 之间满足的关系式是________;
之间满足的关系式是________;
(3)拓展延伸;下面这个一般性的结论成立吗?我们来证明
![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() )
)
证明:设![]() ,
,![]() ,
,
由对数的定义得:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() ).
).
(4)仿照(3)的证明,你能证明下面的一般性结论吗?
![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() ).
).
(5)计算:![]() 的值为________________.
的值为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
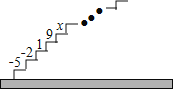
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.
尝试 (1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用含k(k为正整数)的式子表示出数“1”所在的台阶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 y =kx2 +(k +1)x +1(k 为实数),
(1)当 k=3 时,求此函数图象与 x 轴的交点坐标;
(2)判断此函数与 x 轴的交点个数,并说明理由;
(3)当此函数图象为抛物线,且顶点在 x 轴下方,顶点到 y 轴的距离为 2,求 k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
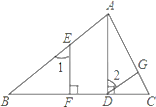
【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com