
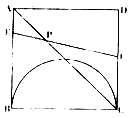
����Ŀ����ͼ��������![]() �У���
�У���![]() Ϊֱ������Բ��
Ϊֱ������Բ��![]() .����������
.����������![]() ��
��![]() ���ֱ�ӵ�
���ֱ�ӵ�![]() ����
����![]() ͬʱ��������
ͬʱ��������![]() ���߶�
���߶�![]() ��
��![]() /����ٶ����
/����ٶ����![]() �˶�����
�˶�����![]() ������
������![]() ��
��![]() /����ٶ����
/����ٶ����![]() �˶�.����
�˶�.����![]() ����
����![]() ��ʱ��
��ʱ��![]() ��
��![]() ͬʱֹͣ�˶�,���
ͬʱֹͣ�˶�,���![]() �˶�ʱ��Ϊ
�˶�ʱ��Ϊ![]() .
.

��1����![]() Ϊ��ֵʱ���߶�
Ϊ��ֵʱ���߶�![]() ��
��![]() ƽ��?
ƽ��?
��2����![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ���Բ���У�
���Բ���У�
��3����ͼ2����ͼ�η���ֱ������ϵ�У���![]() ʱ����
ʱ����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��˫����
��˫����![]() ������
������![]() ���������
���������![]() ���ڵ�
���ڵ�![]() �����˫���ߵĺ�����ϵʽ����ֱ��д��
�����˫���ߵĺ�����ϵʽ����ֱ��д��![]() ��ֵ.
��ֵ.
���𰸡���1����t=![]() ����2����t=
����2����t=![]() ����3����y=��
����3����y=��![]() ��
��![]() .
.
��������
�����������1������ʱ��Ϊt����BE=t��CF=4��2t������BE=CF���t��ֵ����2������ʱ��Ϊt����F����FK��BC����AB��K����BE=t��CF=4��2t��EK=3t��4��EF=4��t������Rt��EKF�Ĺ��ɶ������t��ֵ���ó��𰸣���3������������ó�![]() ��������APE�ס�CPE�ó�
��������APE�ס�CPE�ó�![]() ���Ӷ�˵����P��λ����t����ֵ�أ�����AC�ij������CP�ij��ȣ��Ӷ��ó���P�����꣬���ô���ϵ���������������ʽ���ó���H�����꣬�Ӷ��ó���.
���Ӷ�˵����P��λ����t����ֵ�أ�����AC�ij������CP�ij��ȣ��Ӷ��ó���P�����꣬���ô���ϵ���������������ʽ���ó���H�����꣬�Ӷ��ó���.
�����������1������E��F������t��ʱ��EF��BC��
��ʱBE=t��CF=4��2t��BE=CF����t=4��2t����![]()
��2������E��F������t��ʱ��EF���Բ���У���F����FK��BC����AB��K.
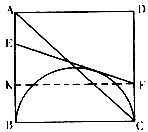
��BE=t��CF=4��2t��EK=EB��KB=EB��FC=t����4��2t��=3t��4 EF=BE+CF�����߳���ȣ�=4��t
��Rt��EKF��EF2=EK2+KF2=��4��t��2=��3t��4��2+22 ���:![]() ��
��![]() ����ȥ��
����ȥ��
��3������1��t��2ʱ����ͼ����![]()
��AB��DC�����APE�ס�CPE ��![]() ����P��λ����t����ֵ��.
����P��λ����t����ֵ��.
��P��λ�ò��ᷢ���仯��AP��PC��ֵΪ![]() ����
����![]() ����AP��PC=1:2�ɵ�CP=
����AP��PC=1:2�ɵ�CP=![]()
��P��![]() ����˫���߽���ʽΪ
����˫���߽���ʽΪ![]() ����P��
����P��![]() �� �����
�� �����![]() ����
����![]()
��H��![]() �� ��
�� ��![]()


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90����AC=8��BC=6��CD��AB�ڵ�D����P�ӵ�D���������߶�DC���C�˶�����Q�ӵ�C���������߶�CA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Cʱ�����㶼ֹͣ�����˶�ʱ��Ϊt����
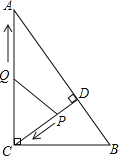
��1�����߶�CD�ij���
��2������CPQ�����ΪS����S��t֮��ĺ�����ϵʽ����ȷ�����˶��������Ƿ����ijһʱ��t��ʹ��
S��CPQ��S��ABC=9��100�������ڣ����t��ֵ���������ڣ���˵��������
��3���Ƿ����ijһʱ��t��ʹ����CPQΪ���������Σ������ڣ������������������t��ֵ���������ڣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������һ������ƽ����һ������������һ��������ƽ����һ������������ƽ�������۸���û����������������ȷ�ĸ����У� ��
A. 0�� B. 1�� C. 2�� D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��y�ķ�����![]() �����Щ�3��a��1�������������⣺
�����Щ�3��a��1�������������⣺
��![]() �Ƿ�����Ľ⣻
�Ƿ�����Ľ⣻
�ڵ�a=��2ʱ��x��y��ֵ��Ϊ�෴����
�۵�a=1ʱ��������Ľ�Ҳ�Ƿ���x+y=4��a�Ľ⣻
����x��1����1��y��4��
������ȷ���������� ������������ȷ�������Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪һ�κ���y=2x+1��ͼ��P1��x1��y1����P2��x2��y2�����㣬��x1��x2����y1 ______ y2�����������������=����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=4������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ������ǣ� ��
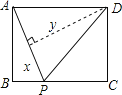
A��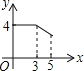 B��
B��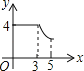 C��
C��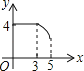 D��
D��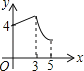
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OΪ����ABCD�Խ��ߵĽ��㣬DE��AC��CE��BD��
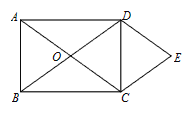
��1�����ж��ı���OCED����״����˵��������
��2����AB=6��BC=8�����ı���OCED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A.��������������������
B.����������������������
C.�������������������ȫ��������
D.һ���������������Ǹ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com