
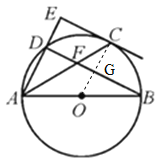
【题目】如图,AB为⊙O的直径,C、D两点均在⊙O上,过点C作CE⊥AD于点E,且AC平分∠BAD.
(1)求证:CE为⊙O的切线;
(2)连结BD交AC于点F,若CF=5,sin∠CAD=![]() ,求线段BD的长.
,求线段BD的长.

【答案】(1)见解析;(2) ![]() .
.
【解析】分析:(1)连结OC交BD于点G.证明∠ECA+∠ACO=90°即可得到结论;
(2)设DF=3x,则AF=5x,AD=4x.由∠CAD=∠ACO,得到sin∠FCG=![]() .进而表示出BG,OG,OB.在Rt△OBG中,由勾股定理得到OB2=OG2+BG2,解方程即可得出结论.
.进而表示出BG,OG,OB.在Rt△OBG中,由勾股定理得到OB2=OG2+BG2,解方程即可得出结论.
详解:(1)连结OC交BD于点G.
∵AC平分∠BAD,∴∠CAD=∠CAB.
又∵OA=OC,∴∠CAB=∠ACO.
又∵CE⊥AD, ∴∠E=90°,∴∠EAC+∠ECA=90°,
∴∠ECA+∠ACO=90°,∴CE为⊙O的切线.
(2)设DF=3x,则AF=5x,AD=4x.
又∵AB为⊙O的直径,∴∠ADB=90°,∴BD∥CE,∴OC⊥BD.
又∵∠CAD=∠ACO,∴sin∠FCG=![]() .
.
又∵CF=5,∴CG=4,FG=3,∴DG=BG=3x+3.
又∵OC∥AE,∴OG=![]() AD=2x,∴OC=OB=4+2x.
AD=2x,∴OC=OB=4+2x.
在Rt△OBG中,OB2=OG2+BG2,∴(4+2x)2=(2x)2+(3x+3)2 ,
∴x=![]() 或-1.
或-1.
又∵x>0,∴x=![]() ,∴BD=2BG=
,∴BD=2BG=![]() .
.


科目:初中数学 来源: 题型:
【题目】完成一项工作,如果安排两个人合做,要![]() 天才能完成.开始先安排一些人做
天才能完成.开始先安排一些人做![]() 天后,又增加
天后,又增加![]() 人和他们一起做
人和他们一起做![]() 天,结果完成了这项工作的一半,假设这些人的工作效率相同.
天,结果完成了这项工作的一半,假设这些人的工作效率相同.
(1)开始安排了多少名工人?
(2)如果要求再用![]() 天做完剩余的全部工作,还需要再增加几人一起做?
天做完剩余的全部工作,还需要再增加几人一起做?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
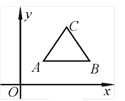
【题目】如图,等边三角形ABC的顶点A、B坐标分别为(1,1)、(3,1),若把等边△ABC先沿x轴翻折,再向左平移1个单位”为第一次変换,则这样连续经过2017次变换后,等边△ABC的顶点C的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平移和翻折是初中数学两种重要的图形变化.
(1)平移运动
①把笔尖放在数轴的原点处,先向负方向移动3个单位长度,再向正方向移动![]() 个单位长度,这时笔尖的位置表示什么数?用算式表示以上过程及结果是( )
个单位长度,这时笔尖的位置表示什么数?用算式表示以上过程及结果是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
②一机器人从原点O开始,第1次向左跳1个单位,紧接着第2次向右跳2个单位,第3次向左跳3个单位,第4次向右跳4个单位,……,依次规律跳,当它跳2019次时,落在数轴上的点表示的数是_____.
(2)翻折变换
①若折叠纸条,表示-1的点与表示3的点重合,则表示2019的点与表示_______的点重合.
![]()
②若数轴上A、B两点之间的距离为2019(A在B的左侧,且折痕与①折痕相同),且A、B两点经折叠后重合,则A点表示_____B点表示______.
③若数轴上折叠重合的两点的数分别为a,b,折叠中间点表示的数为____.(用含有a,b的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目:初中数学 来源: 题型:
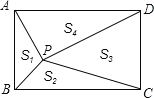
【题目】如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB, △PBC, △PCD, △PDA,的面积分别为![]() ,
,![]() ,
,![]() ,
,![]() ,以下判断: ①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC ;③若
,以下判断: ①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC ;③若![]() =
=![]() ,则
,则![]() =
=![]() ;④若△PAB∽△PDA,则PA=2.4.其中正确的是_____________(把所有正确的结论的序号都填在横线上)
;④若△PAB∽△PDA,则PA=2.4.其中正确的是_____________(把所有正确的结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
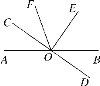
【题目】如图,直线AB和CD交于点O,∠COE=90°,OC平分∠AOF,∠COF=35°.
(1)求∠BOD的度数;
(2)OE平分∠BOF吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
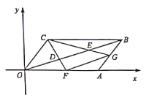
【题目】在平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,点
,点![]() 把线段
把线段![]() 三等分,延长
三等分,延长![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() , 则下列结论:
, 则下列结论:![]() ;
; ![]()
![]() ③四边形
③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ,其中正确的有( ).
,其中正确的有( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com