
【题目】夏季是垂钓的好季节.一天甲、乙两人到松花江的![]() 处钓鱼,突然发现在
处钓鱼,突然发现在![]() 处有一人不慎落入江中呼喊救命.如图,在
处有一人不慎落入江中呼喊救命.如图,在![]() 处测得
处测得![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从
方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从![]() 处跳水游向
处跳水游向![]() 处救人;此时乙从
处救人;此时乙从![]() 沿岸边往正东方向奔跑40米到达
沿岸边往正东方向奔跑40米到达![]() 处,再从
处,再从![]() 处下水游向
处下水游向![]() 处救人,已知
处救人,已知![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
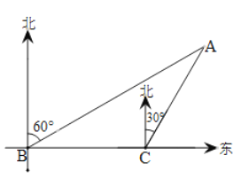
(1)求![]() 、
、![]() 的长.
的长.
(2)试问甲、乙二人谁能先救到人,请通过计算说明理由.(![]() )
)
科目:初中数学 来源: 题型:
【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水 3000 吨,计划内用水每吨收费 0.5元,超计划部分每吨按 0.8 元收费.
(1)写出该单位水费 y(元)与每月用水量 x(吨)之间的函数关系式:(写出自变量取值范围)
①用水量小于等于 3000 吨 ;
②用水量大于 3000 吨 .
(2)某月该单位用水 3200 吨,水费是 元;若用水 2800 吨,水费 元.
(3)若某月该单位缴纳水费 1580 元,则该单位用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,对于下列结论:①△ABE≌△CDF;②AM=MN=NC;③EM=![]() BM,④S△ABM=S△AME,其中正确的有( )
BM,④S△ABM=S△AME,其中正确的有( )
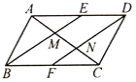
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学以“你最喜欢的运动项目”为主题,对公园里参加运动的群众进行随机调查(每名被调查者只能选一个项目,且被调查者都进行了选择).下面是小明根据调查结果列出的统计表和绘制的扇形统计图(不完整).
被调查者男、女所选项目人数统计表
项目 | 男(人数) | 女(人数) |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|

根据以上信息回答下列问题:
(1)统计表中的![]() __________,
__________,![]() __________.
__________.
(2)扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
(3)若平均每天来该公园运动的人数有3600人,请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上一点,C、D两点分别从P、B出发以1cm/s、2 cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置: ![]()
(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求![]() 的值。
的值。
![]()
(3)在(1)的条件下,若C、D运动5秒后,恰好有![]() ,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②![]() 的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
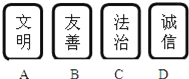
【题目】如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
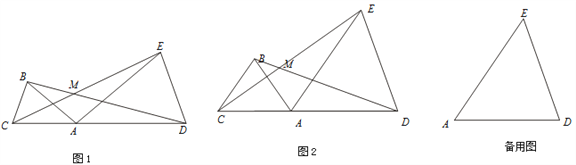
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com