
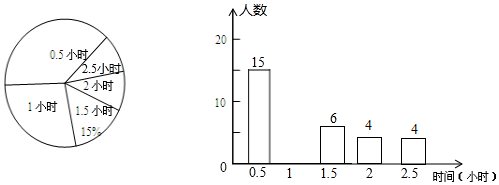
分析 (1)由1.5小时的人数及其百分比可得总人数,总人数减去其它时间的人数求得1小时的人数,即可补全条形图;
(2)根据中位数的定义求解可得;
(3)利用样本中每天参加文体活动的时间不少于1小时的人数所占比例乘以总人数可得.
解答 解:(1)本次调查抽取的老年人共有6÷15%=40(人),
则“1小时”的有40-(15+6+4+4)=11(人),
补全条形图如下: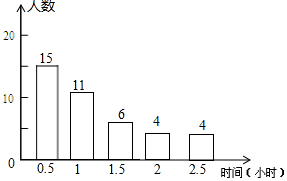
(2)由于共有40个数据,其中位数为第20、21个数据的平均数,
而第20、21个数据均为“1小时”,
∴被调查的老年人中参加文体活动的中位数是1小时;
(3)560×$\frac{11+6+4+4}{40}$=350,
答:估计该街道参加文体活动的老年人中,大约有350人平均每天参加文体活动的时间不少于1小时.
点评 本题考查的是条形统计图和扇形统计图的综合运用及中位数的定义,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了用样本估计总体的思想.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 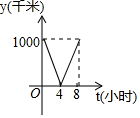 | B. | 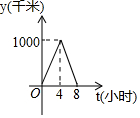 | C. |  | D. | 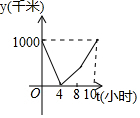 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
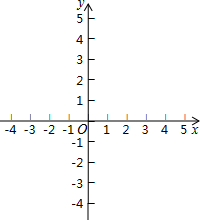 已知点O(0,0),B(1,2).
已知点O(0,0),B(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
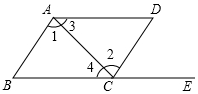 如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )
如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠B=∠DCE | D. | ∠D+∠DAB=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com