
四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.

(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;
(2)如图2,在(1)条件下,AG= BG,求
BG,求 ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE= _________ (直接写出结果)
(1)证明:∵四边形ABCD为矩形,AB=BC,
∴四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
又DE⊥AG,BF∥DE,
∴∠AED=∠AFB=90°,
∵∠BAF+∠DAE=90°,∠BAE+∠ABF=90°,
∴∠DAE=∠ABF,
在△AED和△BFA中,

∴△AED≌△BFA(AAS),
∴AE=BF,
∴AF﹣BF=EF,
(2)如图2,延长AG与DC交于点F,

∵AG= BG,设BG=t,则AG=
BG,设BG=t,则AG= t,
t,
在Rt△ABG中,AB=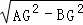 =2t,
=2t,
∴G为BC的中点,
在△ABG和△FCG中,

∴△ABG≌△FCG(AAS),
∴AB=FC=CD,
又∵DE⊥AG,
在Rt△DEF中,C为斜边DF的中点,
∴EC=CD=CF,
∴ =
=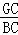 =
=
(3)如图3,连接DG,作EM⊥BC于M点,

∵DE⊥AG,DE=2,GE=1,
∴在RT△DEG中,DG=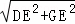 =
= =
= ,
,
∵CG=CD,
∴在RT△DCG中,∠CDG=∠CGD=45°,
∴CD=CG= =
= ,
,
∵∠BAG+∠GAD=90°,∠EDA+∠GAD=90°,
∴∠BAG=∠EDA,
∵∠ABG=∠DEA=90°,
∴△ABG∽△DEA,
∴ =
= ,
,
设AD=x,则AE= =
=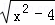 ,AG=
,AG=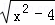 +1,
+1,
∴ =
= ,
,
解得x1= ,x2=﹣2
,x2=﹣2 (舍去)
(舍去)
∴AE= =
=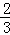 ,
,
又∵∠BAG=∠MEG,
∴∠EDA=∠MEG,
∴△EMG∽△DEA
∴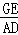 =
= =
= ,即
,即 =
= =
=
解得EM= ,MG=
,MG= ,
,
∴CM=CG+MG= +
+ =
= ,
,
∴CE= =
= =
= .
.
故答案为: .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数为x,y,z,则 +
+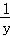 +
+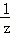 的值为( )
的值为( )
|
| A. | 1 | B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是【 】
A.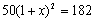 B.
B.
C.50(1+2x)=182 D.
查看答案和解析>>
科目:初中数学 来源: 题型:
某生物实验室需培育一群有益菌.现有60个活体样本,经过两轮培植后,总和达24000个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.每轮分裂中平均每个有益菌可分裂出 个有益菌?
查看答案和解析>>
科目:初中数学 来源: 题型:
旅客乘车按规定可随身携带一定重量的行李,如果超过规定,则需购行李票,设行李费y(元)是行李重量x(千克)的一次函数,其图象如图所示.求:
(1)y与x之间的函数关系式;
(2)旅客最多可免费携带行李的重量.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com