
����Ŀ���׳���![]() �س�������ʻ��
�س�������ʻ��![]() �أ�����
�أ�����![]() �غ�������ԭ·ԭ�ٷ���
�غ�������ԭ·ԭ�ٷ���![]() �أ��ҳ���
�أ��ҳ���![]() �س�������ͬ·������ʻ��
�س�������ͬ·������ʻ��![]() �أ�����
�أ�����![]() Сʱ���ҳ��������;��ͣ��
Сʱ���ҳ��������;��ͣ��![]() Сʱ��Ȼ�������ԭ��ʻ��
Сʱ��Ȼ�������ԭ��ʻ��![]() �أ��ҳ�����ʻ�����е��ٶ���
�أ��ҳ�����ʻ�����е��ٶ���![]() ǧ��/ʱ���׳����ҳ���
ǧ��/ʱ���׳����ҳ���![]() Сʱ����
Сʱ����![]() �أ���������Գ����ص�·��
�أ���������Գ����ص�·��![]() ǧ����׳���ʻʱ��
ǧ����׳���ʻʱ��![]() Сʱ֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ����������⣺
Сʱ֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ����������⣺
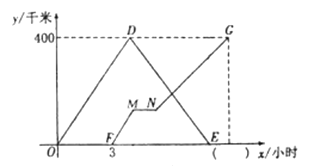
��1��д���׳���ʻ���ٶȣ���ֱ��д��ͼ����������ȷ����__ __
��2����׳���![]() �ط���
�ط���![]() �صĹ����У�
�صĹ����У�![]() ��
��![]() �ĺ�����ϵʽ(����Ҫд���Ա���
�ĺ�����ϵʽ(����Ҫд���Ա���![]() ��ȡֵ��Χ)��
��ȡֵ��Χ)��
��3��ֱ��д���׳���������Сʱ������ǡ�����![]() ǧ�ף�
ǧ�ף�
���𰸡���1��9����2��![]() ����3��
����3��![]() ��1��5Сʱ
��1��5Сʱ
��������
��1����������ͺ���ͼ���е����ݿ�����ü׳���ʻ�ٶȺ�ͼ��������Ӧ��������ݣ�
��2�����ݺ���ͼ���е����ݿ��Եõ��׳���B�ط���A�صĹ����У�y��x�ĺ�����ϵʽ��
��3��������������г���Ӧ�ķ��̣�������Խ����
��1���ҳ���B�ص�A���õ�ʱ��Ϊ��400��80��5��Сʱ����
�׳����ٶ�Ϊ��400��[��3��5��11����2]��100��ǧ��/Сʱ����
ͼ����������ȷ������3��5��1��9��
�ʴ�Ϊ��9��
��2����׳���B�ط���A�صĹ����У�y��x�ĺ�����ϵʽΪy��kx��b��
�ߵ�D��4��400������E��8��0�����߶�DE�ϣ�
��![]() ����
����![]() ��
��
���׳���B�ط���A�صĹ����У�y��x�ĺ�����ϵʽ��y��100x��800��
��3���ټ���B��ǰ�����ҳ�����tСʱ������ǡ�����80ǧ�ף�
80t��100��t��3����40080��
��ã�t��![]() ��
��
�ڵ��ҳ���1Сʱʱ�����ߵ�·����1��80��80��ǧ�ף�����ʱ�պõ��ҵأ����ҵľ����ǣ�80ǧ�ף�
�ҳ���1Сʱ�����ҳ�����tСʱ������ǡ�����80ǧ�ף�
�۵��ҳ���2Сʱʱ�����ߵ�·����1��80��80��ǧ�ף����״�B���ߵ�·���ǣ�100����3��21����100��ǧ�ף�����ʱ���ҵľ����ǣ�10080��20��ǧ�ף���
���׳���B�ط���A�صĹ����У���tСʱ���������80ǧ�ף�
100��t1��80��t1����80��80��t1����80��400��
��ã�t��5��t��5��
���ҳ�����![]() Сʱ��1Сʱ��5Сʱʱ������ǡ�����80ǧ�ף�
Сʱ��1Сʱ��5Сʱʱ������ǡ�����80ǧ�ף�


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
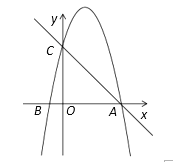
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C����֪B��-1��0���������ߵĶԳ�����ֱ��
��x�ύ��A��B���㣬��y�ύ�ڵ�C����֪B��-1��0���������ߵĶԳ�����ֱ��![]() ��
��
��1��ֱ��д�������ߵĽ���ʽ��
��2����E���߶�AC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���߶�EF�ij������
��3�����������Ƿ���ڵ�P��ʹ����ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺������ۣ�Ͷ���г��������������г����飬���۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ���
![]() ���ÿ�����������
���ÿ�����������![]() Ԫ
Ԫ![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
![]() ������۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
������۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
![]() �������ҵҪʹÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����ô���۵���Ӧ������ʲô��Χ�ڣ�
�������ҵҪʹÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����ô���۵���Ӧ������ʲô��Χ�ڣ�![]() ÿ����ܳɱ�
ÿ����ܳɱ�![]() ÿ���ijɱ�
ÿ���ijɱ�![]() ÿ���������
ÿ���������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶ�����ֱ����һ������ֱ֪�ߵ�ƽ�������ij߹���ͼ����.
��֪��ֱ��![]() ��ֱ��
��ֱ��![]() ��һ��P.
��һ��P.

������ֱ��![]() ��ʹ
��ʹ![]() .
.
��������ͼ��

����ֱ��![]() ��ȡһ��O���Ե�OΪԲ�ģ�
��ȡһ��O���Ե�OΪԲ�ģ�![]() ��Ϊ�뾶����Բ����ֱ��
��Ϊ�뾶����Բ����ֱ��![]() ��
��![]() ���㣻
���㣻
������![]() ����BΪԲ�ģ�
����BΪԲ�ģ�![]() ��Ϊ�뾶����������Բ�ڵ�Q��
��Ϊ�뾶����������Բ�ڵ�Q��
����ֱ��![]() .
.
����ֱ��![]() ������������ֱ��.
������������ֱ��.
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤��
֤��������![]() ��
��
��![]() ��
��
��![]() __________.
__________.
��![]() ��______________���������������ݣ�.
��______________���������������ݣ�.
��![]() ��_____________���������������ݣ�.
��_____________���������������ݣ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �еĵ�P��ͼ��M���������µĶ��壺����ͼ��M����һ��Q��ʹ��P��Q�����ľ���С�ڻ����1�����PΪͼ��M�Ĺ�������
�еĵ�P��ͼ��M���������µĶ��壺����ͼ��M����һ��Q��ʹ��P��Q�����ľ���С�ڻ����1�����PΪͼ��M�Ĺ�������
��1������O�İ뾶Ϊ2ʱ��
���ڵ�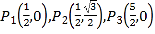 �У���O�Ĺ�������_______________��
�У���O�Ĺ�������_______________��
�ڵ�P��ֱ��y=-x�ϣ���PΪ��O �Ĺ����㣬���P�ĺ������ȡֵ��Χ��
��2����C ��Բ����x���ϣ��뾶Ϊ2��ֱ��y=-x+1��x�ᡢy�ύ�ڵ�A��B�����߶�AB�ϵ����е㶼����C�Ĺ����㣬ֱ��д��Բ��C�ĺ������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P�ǰ뾶Ϊ4����O��һ�㣬PA����O�����ߣ��е�ΪA����PA��4������O������Ϊ4![]() ����AB������PB����PB�ij�Ϊ_____��
����AB������PB����PB�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��ͼ�������ʽ��ac����a+b+c����4a��2b+c����2a+b��ֵ����0�ĸ���Ϊ��������
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD��AB��6��BC��10��E��F�ֱ���AB��BC���е㣬AF��DE�ཻ��I����BD�ཻ��H�����ı���BEIH�����Ϊ��������
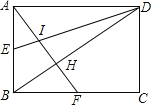
A.6B.7C.8D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ��ѧ�С����ѧϰ�����������Ǻ����������ѡ������С�Ӷ�һ��������BC�ĸ߶ȣ���������б���ϵ�D������ý����ﶥ��B������Ϊ30������D�����ĸ߶�DE=5m���µ�EA=30m��Ȼ����A����ý����ﶥ��B��������60������E��A��C��ͬһˮƽ���ϣ�������BC�ĸߣ�������ú��и��ŵ�ʽ�ӱ�ʾ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com