
分析 (1)利用公式法解方程;
(2)先移项得到(x-3)(x+1)-(x-3)=0,然后利用因式分解法解方程.
解答 解:(1)△=32-4×(-2)=11,
x=$\frac{-3±\sqrt{11}}{2}$,
所以x1=$\frac{-3+\sqrt{11}}{2}$,x2=$\frac{-3-\sqrt{11}}{2}$;
(2)(x-3)(x+1)-(x-3)=0,
(x-3)(x+1-1)=0,
x-3=0或x+1-1=0,
所以x1=3,x2=0.
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法解一元二次方程.


科目:初中数学 来源: 题型:解答题
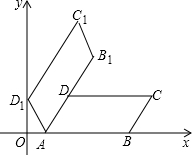 如图,?ABCD的顶点A,B的坐标分别为(1,0),(5,0),∠DAB=60°,AD=2.
如图,?ABCD的顶点A,B的坐标分别为(1,0),(5,0),∠DAB=60°,AD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
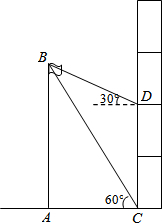 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼五楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=12米,求旗杆AB的高度.
某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼五楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=12米,求旗杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
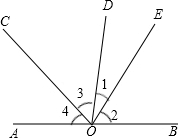 如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠BOE=3∠DOE,∠COE=70°.
如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠BOE=3∠DOE,∠COE=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com