
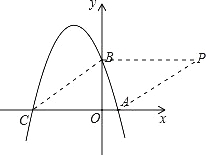
����Ŀ����֪��ͼ����ƽ��ֱ������ϵxOy�У���A��B��C�ֱ�Ϊ���������ϵ������㣬��OA=1��OB=3��OC=4��
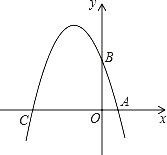
��1����A��B��C����������ߵĽ���ʽ��
��2����ƽ��ֱ������ϵxOy���Ƿ����һ��P��ʹ�����Ե�A��B��C��PΪ������ı���Ϊ���Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3������MΪ����������һ���㣬�ڣ�2���������£��������|PM��AM|�����ֵʱ��M�����꣬��ֱ��д��|PM��AM|�����ֵ��
���𰸡���1��y=��![]() x2��
x2��![]() x+3����2����5��3������3����1��0������5����
x+3����2����5��3������3����1��0������5����![]() �������ֵΪ5.
�������ֵΪ5.
�������������������1���������ߵĽ���ʽΪy=ax2+bx+c����A��B��C��������������a��b��c��ֵ������ȷ�������������߽���ʽ����2����ƽ��ֱ������ϵxOy�д���һ��P��ʹ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�����Ϊ������OA��OB��OC�ij������ù��ɶ������BC��AC�ij���ȣ�ֻ�е�BP��ACƽ�������ʱ���ı���ACBPΪ���Σ��ɵó�BP�ij�����OB�ij�ȷ����P�������꣬ȷ����P���꣬����P�ڵڶ���������ʱ���Ե�A��B��C��PΪ������ı���ֻ����ƽ���ı��Σ��������Σ���3�����ô���ϵ����ȷ����ֱ��PA����ʽ������M���P��A����ͬһֱ����ʱ�����������ε����߹�ϵ|PM��AM|��PA������M���P��A��ͬһֱ����ʱ��|PM��AM|=PA������M���P��A��ͬһֱ����ʱ��|PM��AM|��ֵ�����MΪֱ��PA�������ߵĽ��㣬����ֱ��AP�������߽���ʽ�������|PM��AM|�����ֵʱM���꣬ȷ����|PM��AM|�����ֵ���ɣ�
�����������1���������ߵĽ���ʽΪy=ax2+bx+c�� ��A��1��0��B��0��3��C����4��0����
��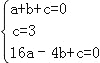 �� ��ã�a=��
�� ��ã�a=��![]() ��b=��
��b=��![]() ��c=3��
��c=3��
������A��B��C����������ߵĽ���ʽΪy=��![]() x2��
x2��![]() x+3��
x+3��
��2����ƽ��ֱ������ϵxOy�д���һ��P��ʹ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�����Ϊ��
��OB=3��OC=4��OA=1�� ��BC=AC=5�� ��BPƽ���ҵ���ACʱ���ı���ACBPΪ���Σ�
��BP=AC=5���ҵ�P��x��ľ������OB�� ����P������Ϊ��5��3����
����P�ڵڶ���������ʱ���Ե�A��B��C��PΪ������ı���ֻ����ƽ���ı��Σ��������Σ�
��P������Ϊ��5��3��ʱ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�
��3����ֱ��PA�Ľ���ʽΪy=kx+b��k��0���� ��A��1��0����P��5��3����
��![]() �� ��ã�k=
�� ��ã�k=![]() ��b=��
��b=��![]() �� ��ֱ��PA�Ľ���ʽΪy=
�� ��ֱ��PA�Ľ���ʽΪy=![]() x��
x��![]() ��
��
����M���P��A����ͬһֱ����ʱ�����������ε����߹�ϵ|PM��AM|��PA��
����M���P��A��ͬһֱ����ʱ��|PM��AM|=PA��
������M���P��A��ͬһֱ����ʱ��|PM��AM|��ֵ�����MΪֱ��PA�������ߵĽ��㣬
�ⷽ����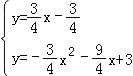 ����
����![]() ��
��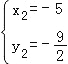 ��
��
����M������Ϊ��1��0������5����![]() ��ʱ��|PM��AM|��ֵ���ʱ|PM��AM|�����ֵΪ5��
��ʱ��|PM��AM|��ֵ���ʱ|PM��AM|�����ֵΪ5��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������д��һ����λ���������λ������ȡ���������е���������ϳ����п��ܵ���λ������6���������������Щ��λ���ĺͣ�Ȼ��������ԭ��λ���ĸ�����λ�ϵ����ĺ�.���磬����λ��223��ȡ����������������п��ܵ���λ����22��23��22��23��32��32.���ǵĺ���154.��λ��223��λ���ĺ���7��![]() �ٻ���������һ�ԣ��㷢����ʲô����д���㰴���淽����̽�����̺������ֵĽ���������ô���ʽ��֪ʶ˵�������ֵĽ������ȷ��.
�ٻ���������һ�ԣ��㷢����ʲô����д���㰴���淽����̽�����̺������ֵĽ���������ô���ʽ��֪ʶ˵�������ֵĽ������ȷ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ����̽��
��![]()
��![]()
��![]()
����
��1��д���ڢܸ���ʽ��______��
��2��ijͬѧ���֣��ĸ�������Ȼ���Ļ�����1���������ijһ��������ƽ���������ĸ����ϴ�ʱ���Խ��м����㣬�磺
![]() ��
��
�������д����n����ʽ���ú���n�Ĵ���ʽ��ʾ����ͨ��������֤��IJ��룮
��3���κ�ʵ����ƽ�����ǷǸ�������![]() ����һ���Ǹ�����һ�������ĺͱض���һ����������
����һ���Ǹ�����һ�������ĺͱض���һ����������![]() ʱ��
ʱ��![]() �����������ϵĹ��ɺͷ�����˵��������xΪʲôʵ��������ʽ
�����������ϵĹ��ɺͷ�����˵��������xΪʲôʵ��������ʽ![]() ��ֵ��Զ����������
��ֵ��Զ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���ax2+bx+c=0��a��0���У�����˵����
����a+b+c=0����b2��4ac��0��
��������������1��2����2a+c=0��
��������ax2+c=0����������ȵ�ʵ������ax2+bx+c=0������������ȵ�ʵ����
����b=2a+c��������������ȵ�ʵ����������ȷ���У�������
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ŵ���ѧ��������һԪ���η�������x2��2x��3=0Ϊ�������¹������£���һ������ԭ���̱���Ϊx2��2x=3����x��x��2��=3��
�ڶ���������һ����Ϊx����Ϊ��x��2���ij����Σ����ȿ���2�������Ϊ3����ͼ��ʾ��
�����������ĸ������ij�����Χ��һ���������Σ��м���һ��С�����Σ���ͼ��ʾ��
���IJ�������������������x��ʾΪ���� ���������������Ϊ�������� ��С���������Ϊ�������� ��
�ɹ۲�ɵã�����������������ĸ���������С���������֮�ͣ��÷������� �������߿�������ã�x1=3��x2=��1��
��1�����IJ��к�����Ӧ�������� ���������� ���������� ���������� ������
��2����ο����˵�˼�����̣�����ʾ��ͼ��д�����裬�ⷽ��x2��x��1=0��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�Ķ���A�ڵ�һ���ޣ�AB��x�ᣬAD��y�ᣬ�ҶԽ��ߵĽ�����ԭ��O�غϣ��ڱ�AB��С��AD������AD�ı仯�����У�������ABCD���ܳ�ʼ�ձ��ֲ��䣬������A�ķ���������y=![]() ��k��0����k��ֵ�ı仯����ǣ� ��
��k��0����k��ֵ�ı仯����ǣ� ��
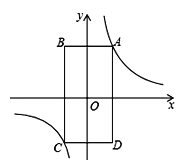
A. һֱ���� B. һֱ��С C. ��������С D. �ȼ�С������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��2016����ҵ��ˮ��x���֣������Ӧ����ˮ��y��Ԫ��֮��ĺ�����ϵ��ͼ��

��1����x��50ʱ����y����x�ĺ�����ϵʽ��
��2����ij��ҵ2016��10�·ݵ�ˮ��Ϊ620Ԫ�������ҵ2016��10�·ݵ���ˮ����
��3��Ϊ������ҵ��Լ��ˮ��������2017��1�¿�ʼ������ˮ������80�ֵ���ҵ������ˮ�����ѣ��涨������ҵ����ˮ��x����80�֣������2016���շѱ���ȡˮ���⣬����80�ֵIJ���ÿ��������![]() Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
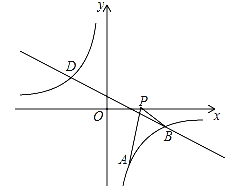
����Ŀ����ͼ����֪��A��1��a���Ƿ���������![]() ��ͼ����һ����ֱ��
��ͼ����һ����ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ��Ľ���Ϊ��B��D����B��3����1��������
��ͼ��Ľ���Ϊ��B��D����B��3����1��������
��1�����������Ľ���ʽ��
��2�����D��������ֱ��д��y1��y2ʱx��ȡֵ��Χ��
��3������P��x��0����x������������˶������߶�PA���߶�PB֮��ﵽ���ʱ�����P��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ������
������![]() ��������
��������![]() �ֱ���
�ֱ���![]() ���
���![]() ���ϣ���֪��
���ϣ���֪��![]() ����
����![]() .
.
(1)���Ѿ���![]() ��ֱ��
��ֱ��![]() �۵���ʹ��
�۵���ʹ��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() ��
��![]() �Ľ���ֱ�Ϊ
�Ľ���ֱ�Ϊ![]() �����ۺ�
�����ۺ�![]() �ij���
�ij���
(2)��(1)�������£���![]() ��
��![]() ���ϣ���ƽ�����Ƿ���ڵ�
���ϣ���ƽ�����Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊ������ı��������Σ������ڣ����������
Ϊ������ı��������Σ������ڣ����������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
(3)��ͼ![]() ����
����![]() Ϊ
Ϊ![]() ���ϵ�һ���㣬��
���ϵ�һ���㣬��![]() ��ȡһ��
��ȡһ��![]() ��������
��������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����תһ�ܣ�����ת�Ĺ����У�
˳ʱ����תһ�ܣ�����ת�Ĺ����У�![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ����ֱ��д��
����ֱ��д��![]() �����ֵ����Сֵ.
�����ֵ����Сֵ.


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com