
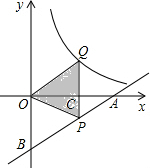
 如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{5}{x}$(x>0)的图象于Q,则S△OQP=$\frac{7}{2}$.
如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{5}{x}$(x>0)的图象于Q,则S△OQP=$\frac{7}{2}$. 分析 首先根据y=$\frac{1}{2}$x-2可以求出A、B两点坐标,接着求出OA,OB长,由PC为△AOB的中位线可以推出OC=$\frac{1}{2}$OA=2,PC=$\frac{1}{2}$OB=1,可求S△OPC,根据反比例函数系数k的意义可求S△OQC,进一步可得S△OQP.
解答 解:∵y=$\frac{1}{2}$x-2分别交x轴、y轴于A、B两点,
∴A(4,0),B(0,-2),
∵PC为△AOB的中位线,
∴OC=$\frac{1}{2}$OA=2,PC=$\frac{1}{2}$OB=1,
∴S△OPC=$\frac{1}{2}$×2×1=1,
又∵反比例函数y=$\frac{5}{x}$(x>0),
∴S△OQC=$\frac{5}{2}$,
∴S△OQP=S△OPC+S△OQC=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 此题难度较大,考查了反比例函数系数k的意义、中位线定理及三角形面积公式,综合性比较强.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
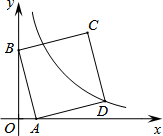 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么:
如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com