
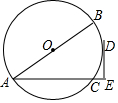
 如图,已知⊙O的直径AB=12,弦AC=10,D是$\widehat{BC}$的中点,过点D作DE⊥AC,交AC的延长线于点E.
如图,已知⊙O的直径AB=12,弦AC=10,D是$\widehat{BC}$的中点,过点D作DE⊥AC,交AC的延长线于点E.分析 (1)连接OD,由D为弧BC的中点,得到两条弧相等,进而得到两个同位角相等,确定出OD与AE平行,利用两直线平行同旁内角互补得到OD与DE垂直,即可得证;
(2)过O作OF垂直于AC,利用垂径定理得到F为AC中点,再由四边形OFED为矩形,求出FE的长,由AF+EF求出AE的长即可.
解答 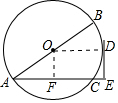 (1)证明:连接OD,
(1)证明:连接OD,
∵D为$\widehat{BC}$的中点,
∴$\widehat{BD}$=$\widehat{CD}$,
∴∠BOD=∠BAE,
∴OD∥AE,
∵DE⊥AC,
∴∠ADE=90°,
∴∠AED=90°,
∴OD⊥DE,
则DE为圆O的切线;
(2)解:过点O作OF⊥AC,
∵AC=10,
∴AF=CF=$\frac{1}{2}$AC=5,
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED为矩形,
∴FE=OD=$\frac{1}{2}$AB,
∵AB=12,
∴FE=6,
则AE=AF+FE=5+6=11.
点评 此题考查了切线的性质与判定,勾股定理,以及垂径定理,熟练掌握各自的性质及定理是解本题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:选择题
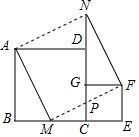 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b-$\frac{{b}^{2}}{a}$;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b-$\frac{{b}^{2}}{a}$;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 567×103 | B. | 56.7×104 | C. | 5.67×105 | D. | 0.567×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
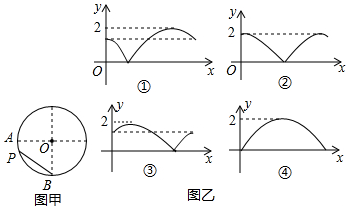
| A. | ① | B. | ③ | C. | ②或④ | D. | ①或③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对重庆市初中学生每天阅读时间的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某批次手机的防水功能的调查 | |
| D. | 对某校九年级3班学生肺活量情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
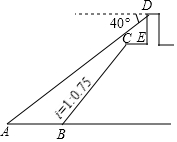 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).| A. | 5.1米 | B. | 6.3米 | C. | 7.1米 | D. | 9.2米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com