
 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
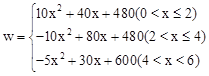 ;(3)该公司每年国内、国外的销售量各为4千件、2千件,可使公司每年的总利润最大,最大值为64万元.
;(3)该公司每年国内、国外的销售量各为4千件、2千件,可使公司每年的总利润最大,最大值为64万元.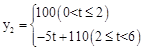 以及t=6-x即可求出y2与x的函数关系:当0<x≤4时,y2=5x+80;当y2=100时,
以及t=6-x即可求出y2与x的函数关系:当0<x≤4时,y2=5x+80;当y2=100时, ,即
,即 ,解得
,解得 ;(2)根据总利润=国内销售的利润+国外销售的利润,结合函数解析式,分三种情况讨论:①0<x≤2;②2<x≤4;③4<x<6;(3)先利用配方法将各解析式写成顶点式,再根据二次函数的性质,求出三种情况下的最大值,再比较即可.
;(2)根据总利润=国内销售的利润+国外销售的利润,结合函数解析式,分三种情况讨论:①0<x≤2;②2<x≤4;③4<x<6;(3)先利用配方法将各解析式写成顶点式,再根据二次函数的性质,求出三种情况下的最大值,再比较即可.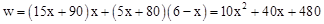 ;
; ;
; .
.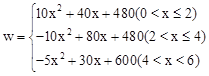 .
. ,此时x=2时,w最大=600;
,此时x=2时,w最大=600; ,此时x=4时,w最大=640;
,此时x=4时,w最大=640; ,∴4<x<6时,w<640.
,∴4<x<6时,w<640.

 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com