
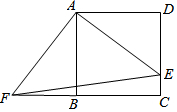
 如图,四边形ABCD是正方形,E、F分别是边DC和CB延长线上的点,且DE=BF,连接AE,AF,EF
如图,四边形ABCD是正方形,E、F分别是边DC和CB延长线上的点,且DE=BF,连接AE,AF,EF分析 (1)根据正方形的性质得AD=AB,∠D=∠ABC=90°,然后利用“SAS”证得△ADE≌△ABF;
(2)根据旋转的定义,可得到△ABF可以由△ADE绕旋转中心 A点,按逆时针方向旋转270度得到;
(3)根据全等三角形的面积相等,可得四边形AFCE的面积等同于正方形ABCD的面积,再根据正方形的边长求得正方形的面积即可.
解答  解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,
∴∠ABF=90°,
在△ADE和△ABF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABF=∠ADE}\\{BF=DE}\end{array}\right.$,
∴△ADE≌△ABF(SAS);
(2)△ABF可以由△ADE绕旋转中心点A,按顺时针方向旋转90度得到.
故答案为:A,90;
(3)由旋转可得,AF=AE=10,而DE=6,
∴Rt△ADE中,AD=$\sqrt{A{E}^{2}-D{E}^{2}}$=8,
∴正方形ABCD的面积为64,
∵△ADE≌△ABF,
∴四边形AFCE的面积=正方形ABCD的面积,
∴四边形AFCE的面积为64.
点评 本题主要考查了旋转的性质,全等三角形的判定与性质以及正方形的性质的运用,解题时注意:旋转前、后的图形全等;正方形的四条边都相等,四个角都是直角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
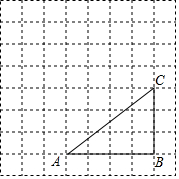 如图,将△ABC放在由小正方形构成的网格图中,点A、B、C均落在格点上.
如图,将△ABC放在由小正方形构成的网格图中,点A、B、C均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
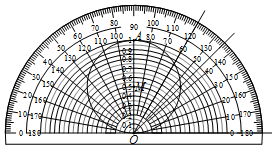 利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )
利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )| A. | 70° | B. | 50° | C. | 40° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
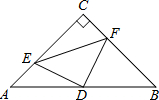 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com