
【题目】下图的方格纸中有若干个点,若A、B两点关于过某点的直线对称,这个点可能是( ).
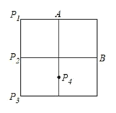
A.P1B.P2C.P3D.P4
【答案】C
【解析】
根据两点的对称轴即两点连线的垂直平分线,利用勾股定理分别求出选项中各点到A、B的距离,再根据垂直平分线的性质即可判断.
解:连接P1B,P2A,P3A,P3B,P4B,设正方形的边长为1,P4O=a,如下图所示
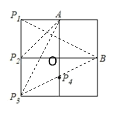
∵A、B两点关于过某点的直线对称
∴此点在AB的垂直平分线上
∴此点到A、B的距离相等
由图可知:P1A=1
根据勾股定理:P1B=![]()
∴P1A≠P1B,故A选项不符合题意;
由图可知:P2B=2
根据勾股定理:P2A=![]()
∴P2B≠P2A,故B选项不符合题意;
根据勾股定理:P3A=![]()
P3B=![]()
∴P3A= P3B,故C选项符合题意;
由图可知P4A=1+a
根据勾股定理:P4B=![]()
当P4A=P4B时,即1+a=![]()
解得:a=0(与图不符)
∴P4A≠P4B,故D选项不符合题意.
故选C.


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数![]() (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.
(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
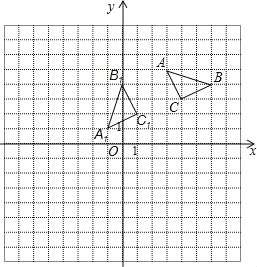
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为8元/千克的水果,经试销发现,销量y(千克)与销售单价x(元)符合一次函数y=kx+b,且当x=10时,y=300;当x=13时,y=150.
(1)求y(千克)与x(元)(x>8)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个边长为a的大正方形和四个边长为b的全等的小正方形(其中a>2b),按如图方式摆放,并顺次连接四个小正方形落入大正方形内部的顶点,得到四边形ABCD.
下面有四种说法:
①阴影部分周长为4a;
②阴影部分面积为(a+2b)(a-2b);
③四边形ABCD周长为8a-4b;
④四边形ABCD的面积为a24ab4b2.
所有合理说法的序号是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的直角坐标系中,已知点A(2,0)、B(0,-4),将线段AB绕点A按逆时针方向旋转90°至AC.

(1)求点C的坐标;
(2)若抛物线y=-x2+ax+4经过点C.
①求抛物线的解析式;
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.

(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com