
【题目】若关于x的一元二次方程kx2﹣2x+1=0有实数根,则k的取值范围是 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系式y=a(x﹣h)2+k,二次函数y=a(x﹣h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为﹣16、20.
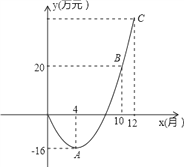
(1)试确定函数关系式y=a(x﹣h)2+k;
(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
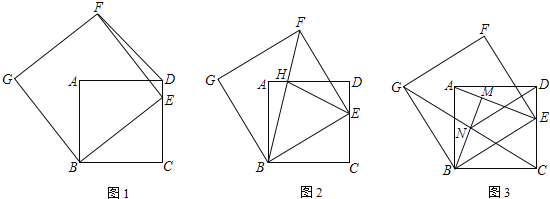
【题目】如图1,E为边长为1的正方形ABCD中CD边上的一动点(不含点C、D),以BE为边作图中所示的正方形BEFG
(1)求∠ADF的度数
(2)如图2,若BF交AD于点H,连接EH,求证:HB平分∠AHE
(3)如图3,连接AE、CG,作BM⊥AE于点M,BM交GC于点N,连接DN.当E在CD上运动时,求证:NC=NG
查看答案和解析>>
科目:初中数学 来源: 题型:
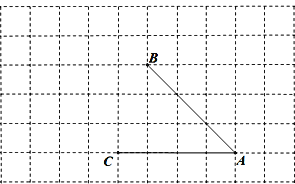
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线
的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店把某种“大运”纪念品按成本价提高50%后标价,又以8折(即按标价的80%优惠售出,结果每件仍获利2.4元,则这种纪念品的成本是
A.3元B.4.8元C.6元D.12元
查看答案和解析>>
科目:初中数学 来源: 题型:
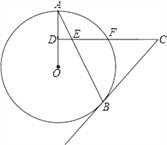
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com