如图所示，已知二次函数
经过
、
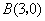、C三点，点
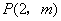是抛物线与直线
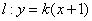的一个交点．
（1）求二次函数关系式和点C的坐标；
（2）对于动点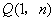
，求
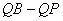的最大值；
（3）若动点M在直线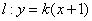上方的抛物线运动，过点M做x轴的垂线交x轴于点F，如果直线AP把线段MF分成1:2的两部分，求点M的坐标。
 |
科目：初中数学 来源： 题型：
如图2212，半圆O的直径AB＝4，与半圆O内切的动圆O1与AB切于点M，设⊙O1的半径为y，AM＝x，则y关于x的函数关系式是( )
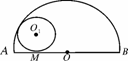
图2212
A．y＝－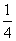
x2＋x B．y＝－x2＋x
C．y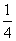＝－x2－x D．y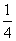＝x2－x
查看答案和解析>>
科目：初中数学 来源： 题型：
某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润y(单位：元/千度)与电价x(单位：元/千度)的函数关系式为y＝－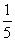
x＋300(x≥0)．
(1)当电价为600元千度时，工厂消耗每千度电产生利润是多少？
(2)为了实现节能减排目标，有关部门规定，该厂电价x(单位：元/千度)与每天用电量m(单位：千度)的函数关系为x＝10m＋500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
“低碳生活，绿色出行”，自行车正逐渐成为人们喜爱的交通工具．某运动商城的自行车销售量自2013年起逐月增加，据统计，该商城1月份销售自行车64辆，3月份销售了100辆．
（1）若该商城前4个月的自行车销量的月平均增长率相同，问该商城4月份卖出多少辆自行车？
（2）考虑到自行车需求不断增加，该商城准备投入3万元再购进一批两种规格的自行车，已知A型车的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆．根据销售经验，A型车不少于B型车的2倍，但不超过B型车的2.8倍．假设所进车辆全部售完，为使利润最大，该商城应如何进货？
查看答案和解析>>
科目：初中数学 来源： 题型：
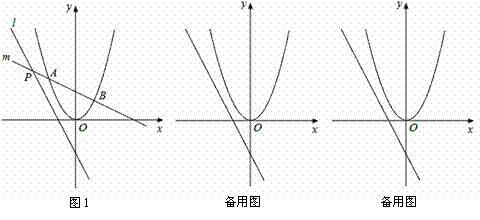
如图1，点P是直线l：y=－2x－2上的点，过点P的另一条直线m交抛物线y=x2于A、B两点．
（1）若A(－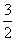
，n)、B(1，1)，求直线m的解析式；
（2）若P(
－2，t)，当PA＝AB时，求点A的坐标；
（3）无论点P在l上移动到何处，是否总可以找到这样的直线，使得PA＝AB？若存在，请给予证明，若不存在，请说明理由．
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系xOy中，以点A（2，3）为顶点作一直角∠PAQ，使其两边分别与x轴、y轴的正半轴交于点P，Q．连接PQ，
过点A作AH⊥PQ于点H．如果点P的横坐标为x，
AH的长为y，那么在下列图象中，能表示y与x的
函数关系的图象大致是（ ）
A B C D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
;
，所以动点Q（1，n)在二次函数的对称轴上。 所以当点Q、P、B三点共线时，
把x=2代入
﹣
= ．
．