
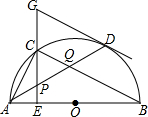
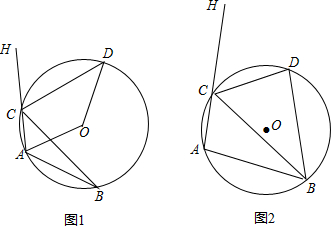
 如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:
如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:分析 由于$\widehat{AC}$与$\widehat{BD}$不一定相等,根据圆周角定理可知①错误;连接OD,利用切线的性质,可得出∠GPD=∠GDP,利用等角对等边可得出GP=GD,可知②正确;先由垂径定理得到A为$\widehat{CE}$的中点,再由C为$\widehat{AD}$的中点,得到$\widehat{CD}$=$\widehat{AE}$,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ为直角,由等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,可知③正确;
解答 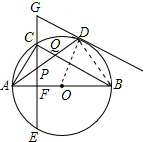 解:∵在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,
解:∵在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,
∴$\widehat{AC}$=$\widehat{CD}$≠$\widehat{BD}$,
∴∠BAD≠∠ABC,故①错误;
连接OD,
则OD⊥GD,∠OAD=∠ODA,
∵∠ODA+∠GDP=90°,∠EPA+∠FAP=∠FAP+∠GPD=90°,
∴∠GPD=∠GDP;
∴GP=GD,故②正确;
∵弦CE⊥AB于点F,
∴A为$\widehat{CE}$的中点,即$\widehat{AE}$=$\widehat{AC}$,
又∵C为$\widehat{AD}$的中点,
∴$\widehat{AC}$=$\widehat{CD}$,
∴$\widehat{AE}$=$\widehat{CD}$,
∴∠CAP=∠ACP,
∴AP=CP.
∵AB为圆O的直径,
∴∠ACQ=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故③正确;
故答案为:②③.
点评 本题考查了圆周角定理,垂径定理,圆心角、弧、弦的关系定理,相似三角形的判定与性质,以及三角形的外接圆与圆心,平行线的判定,熟练掌握性质及定理是解决本题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
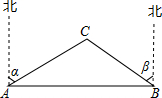 如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.
如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
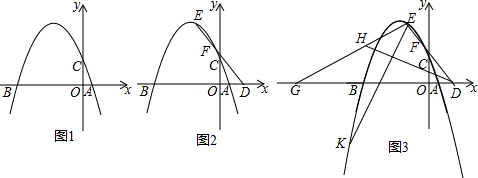
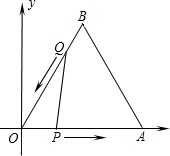 如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:
如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com