
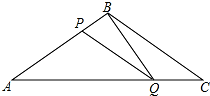
 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从点C出发,沿CA以3cm/s的速度向点A运动,当其中一点到达终点时,另一点也停止运动,设运动时间为x(s).
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从点C出发,沿CA以3cm/s的速度向点A运动,当其中一点到达终点时,另一点也停止运动,设运动时间为x(s).分析 (1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.
(2)由三角形的面积关系得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出三角形BPQ和三角形ABC的面积比.
(3)分两种情况进行讨论.由等腰三角形的性质得出∠A和∠C对应相等,那么就要分成AP和CQ对应成比例以及AP和BC对应成比例两种情况.
解答 解:(1)当PQ∥BC时,AP:AB=AQ:AC,
∵AP=4x,AQ=30-3x,
∴$\frac{4x}{20}$=$\frac{30-2x}{30}$,
解得:x=$\frac{10}{3}$;
即当x=$\frac{10}{3}$,PQ∥BC;
(2)∵S△BCQ:S△ABC=1:3
∴CQ:AC=1:3,
∴CQ=10c,
∴时间用了 $\frac{10}{3}$秒,
∴AP=$\frac{40}{3}$cm,
∵由(1)知,此时PQ∥BC,
∴△APQ∽△ABC,相似比为 $\frac{2}{3}$,
∴S△APQ:S△ABC=4:9,
∴四边形PQCB与三角形ABC面积比为5:9,即S四边形PQCB=$\frac{5}{9}$S△ABC,
又∵S△BCQ:S△ABC=1:3,即S△BCQ=$\frac{1}{3}$S△ABC,
∴S△BPQ=S四边形PQCB-S△BCQ═$\frac{5}{9}$S△ABC-$\frac{1}{3}$S△ABC=$\frac{2}{9}$S△ABC,
∴S△BPQ:S△ABC=2:9;
(3)能.
①当△APQ∽△CQB时,有 $\frac{AP}{CQ}$=$\frac{AQ}{BC}$ 即:$\frac{4x}{3x}$=$\frac{30-3x}{20}$ 解得:x=$\frac{10}{9}$(秒),
∴AP=4x=$\frac{40}{9}$ (cm)
②当△APQ∽△CBQ时,有 $\frac{AP}{CB}$=$\frac{AQ}{CQ}$ 即:$\frac{4x}{20}$=$\frac{30-3x}{3x}$ 解得:x=5(秒)或x=-10(秒)(舍去)
∴PA=4x=20(cm),
综上所述,当AP=$\frac{40}{9}$cm或20cm时,△APQ与△CQB相似.
点评 本题是相似形综合题目,主要考查了相似三角形的判定和性质、平行线分线段成比例定理;根据三角形相似得出线段比或面积比是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
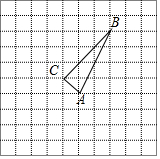 如图在10×10的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
如图在10×10的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 第一个月 | 第二个月 | 清仓时 | |
| 单价(元) | 80 | 80-x | 40 | |
| 销售量(件) | 200 | 200+10x | 400-10x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com