
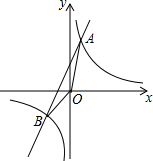
 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).分析 (1)根据待定系数法即可解决问题.
(2)直线AB与y轴交于点C(0,2),根据S△ABO=S△BOC+S△AOC即可解决问题.
(3)根据y1≤y2时,反比例函数图象在一次函数图象下面,写出自变量取值范围即可.
解答  解:(1)把点A(1,4)代入y1=$\frac{k}{x}$,得到k=4,
解:(1)把点A(1,4)代入y1=$\frac{k}{x}$,得到k=4,
∴y1=$\frac{4}{x}$,把点B(m,-2)代入得到,m=-2,
把A(1,4)和点B(-2,-2)代入y2=ax+b得到$\left\{\begin{array}{l}{a+b=4}\\{-2a+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,
∴y2=2x+2.
(2)直线AB与y轴交于点C(0,2),
∴S△ABO=S△BOC+S△AOC=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×1=3.
(3)由图象可知得y1≤y2成立的自变量x的取值范围:x≥1或-2≤x<0.
点评 本题考查一次函数与反比例函数图象的交点,待定系数法,解题的关键是灵活运用待定系数法确定函数解析式,学会利用图象确定自变量取值范围,属于中考常考题型.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:填空题
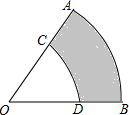 如图,已知扇形OAB与扇形OCD是同心圆,OA=R,OC=r.
如图,已知扇形OAB与扇形OCD是同心圆,OA=R,OC=r.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
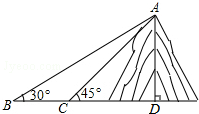 如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.73)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com