
已知:如图,直线 交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(1)求b的值;
(2)若点P是线段AB中垂线上的点,是否存在这样的点P,使△PBC成为直角三角形.若存在,试直接写出所有符合条件的点P的坐标;若不存在,试说明理由;
(3)点Q为线段AB上一个动点(点Q与点A、B不重合),QE∥AC,交BC于点E,以QE为边,在点B的异侧作正方形QEFG.设AQ=m,△ABC与正方形QEFG的重叠部分的面积为S,试求S与m之间的函数关系式,并写出m的取值范围.
(1)4;(2)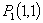 ,
,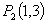 ,
,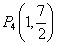 ,
,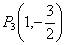 ;(3)
;(3)
解析试题分析:(1)先求得OB、OC的长,再由AO=BO可得点A的坐标,再根据三角形的面积公式求解;
(2)题目中没有明确直角,故要分情况讨论,再结合直角三角形的性质求解即可;
(3)设正方形QEFG与AC相交于点M,先求得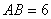 ,在Rt△AOC中,根据勾股定理可求得AC的长,由EQ∥AC可得
,在Rt△AOC中,根据勾股定理可求得AC的长,由EQ∥AC可得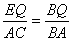 ,即可表示出
,即可表示出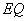 的长,证得△QMA为等腰直角三角形,可得QM=
的长,证得△QMA为等腰直角三角形,可得QM= ,当
,当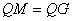 时,正方形QEFG的边FG恰好与AC共线,此时
时,正方形QEFG的边FG恰好与AC共线,此时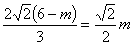 ,解得
,解得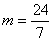 ,再分当0<m≤
,再分当0<m≤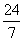 、
、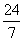 <m<6两种情况分析即可.
<m<6两种情况分析即可.
(1)由题意得:B(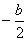 ,0),C(0,b)
,0),C(0,b)
∴OB=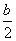 ,OC=b
,OC=b
∵AO=BO
∴A(b,0).
∴OA=b,AB=b+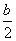 =
=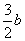
∵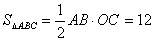
∴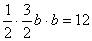
解得:b1=4,b2=-4(舍去)
∴b=4;
(2)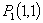 ,
,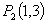 ,
,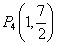 ,
,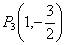 ;
;
(3)如图,设正方形QEFG与AC相交于点M.
∵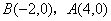
∴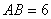
在Rt△AOC中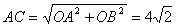
∵EQ∥AC
∴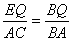
∴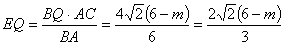
∵EQ∥AC
∴∠AMQ=∠EQM=90°,∠MAQ=45°
∴△QMA为等腰直角三角形
∴QM=
当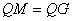 时,正方形QEFG的边FG恰好与AC共线
时,正方形QEFG的边FG恰好与AC共线
此时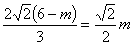 ,解得
,解得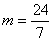
当0<m≤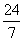 时,
时,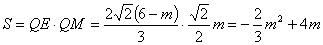
当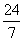 <m<6时,
<m<6时,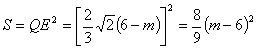
∴S与m之间的函数关系式为 .
.
考点:动点的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


科目:初中数学 来源: 题型:
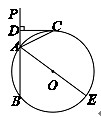
已知:如图,直线![]() 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作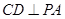 于D.
于D.
1.求证:CD为⊙O的切线;
2.若DC+DA=6,⊙O的直径为10,求AB的长.
查看答案和解析>>
科目:初中数学 来源:2012年浙江省湖州市中考数学一模试卷(解析版) 题型:解答题
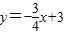 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.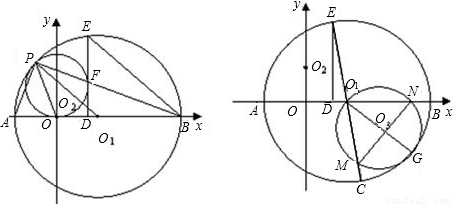
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《图形的相似》(04)(解析版) 题型:解答题
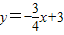 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.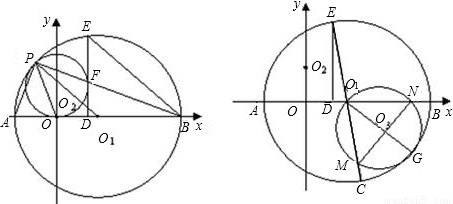
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《圆》(12)(解析版) 题型:解答题
 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省南通市通州区九年级中考适应性考试(一模)数学试卷(解析版) 题型:解答题
已知:如图,直线 交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.

(1)求b的值;
(2)若点P是线段AB中垂线上的点,是否存在这样的点P,使△PBC成为直角三角形.若存在,试直接写出所有符合条件的点P的坐标;若不存在,试说明理由;
(3)点Q为线段AB上一个动点(点Q与点A、B不重合),QE∥AC,交BC于点E,以QE为边,在点B的异侧作正方形QEFG.设AQ=m,△ABC与正方形QEFG的重叠部分的面积为S,试求S与m之间的函数关系式,并写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com