【题目】如图，在四边形ABCD中，点E，F分别是AD，BC的中点，G，H分别是BD，AC的中点，AB，CD满足什么条件时，四边形EGFH是菱形？请证明你的结论．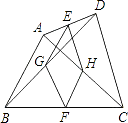 
【答案】解：当AB=CD时，四边形EGFH是菱形． 证明：∵点E，G分别是AD，BD的中点，
∴EG 
AB，同理HF AB，∴EG 
HF．
∴四边形EGFH是平行四边形．
∵EG= 
AB，又可同理证得EH= CD，
∵AB=CD，∴EG=EH，
∴四边形EGFH是菱形
【解析】本题可根据菱形的定义来求解．E、G分别是AD，BD的中点，那么EG就是三角形ADB的中位线，同理，HF是三角形ABC的中位线，因此EG、HF同时平行且相等于AB，因此EG∥=HF． 因此四边形EHFG是平行四边形，E、H是AD，AC的中点，那么EH= 
CD，要想证明EHFG是菱形，那么就需证明EG=EH，那么就需要AB、CD满足AB=CD的条件．
【考点精析】关于本题考查的三角形中位线定理和菱形的判定方法，需要了解连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能得出正确答案．
科目：初中数学 来源： 题型：
【题目】餐桌桌面是长为160cm，宽为100cm的长方形，妈妈准备设计一块桌布，面积是桌面的2倍，且使四周垂下的边等宽．若设垂下的桌布宽为xcm，则所列方程为（ ）
A.（160+x）（100+x）=160×100×2
B.（160+2x）（100+2x）=160×100×2
C.（160+x）（100+x）=160×100
D.2（160x+100x）=160×100
查看答案和解析>>
科目：初中数学 来源： 题型：
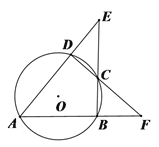
【题目】如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F．
（1）若∠E=∠F时，求证：∠ADC=∠ABC；
（2）若∠E=∠F=42°时，求∠A的度数；
（3）若∠E= 
，∠F= 
，且
≠
．请你用含有
、
的代数式表示∠A的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B =∠E=30°．
（1）操作发现
如图2，固定△ABC，使△DEC绕点C旋转．当点D恰好落在AB边上时，填空：
线段DE与AC的位置关系是 ；
设△BDC的面积为
，△AEC的面积为
，则
与
的数量关系是 ．
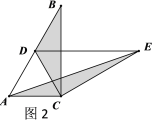
（2）猜想论证
当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中
与
的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高DM和AN，请你证明小明的猜想．
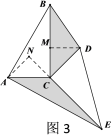
（3）拓展探究
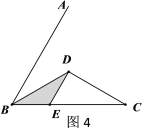
已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使
，请求出相应的BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
小丁在研究数学问题时遇到一个定义：对于按固定顺序的
个数： 
， 
， 
， 
， 
，称为数列
， 
， 
， 
， 
，其中
为整数且
．
定义
．
例如，若数列
， 
， 
， 
， 
，则
．
根据以上材料，回答下列问题：
（
）已知数列
， 
， 
，求
．
（
）已知数列
， 
， 
， 
中
个数均为非负数，且
，直接写出
的最大值和最小值．
（
）已知数列
， 
， 
， 
，其中
， 
， 
， 
，为
个整数，且
， 
， 
，直接写出所有可能的数列
中至少两种．
查看答案和解析>>
科目：初中数学 来源： 题型：
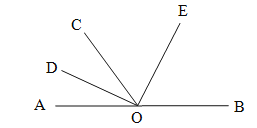
【题目】如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°．
（1）请你数一数，图中有多少个小于平角的角？分别是哪些角？
（2）求∠DOB的度数；
（3）请你通过计算说明OE是否平分∠COB？
查看答案和解析>>
科目：初中数学 来源： 题型：
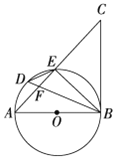
【题目】如图，AB是⊙O的直径，点D是弧AE上一点，且∠BDE=∠CBE，BD与AE交于点F.
（1）求证：BC是⊙O的切线；
（2）若BD平分∠ABE，求证：DE2=DF·DB；
（3）在（2）的条件下，延长ED，BA交于点P，若PA=AO，DE=2，求PD的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com