
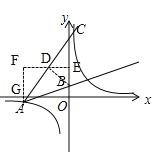
【题目】如图,已知点B(0,2),A(﹣6,﹣1)在反比例函数![]() 的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数
的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数![]() 图象于点C,则点C的坐标为_____.
图象于点C,则点C的坐标为_____.

【答案】(![]() ,18)
,18)
【解析】
过B作BD⊥AC于D,过D作DE⊥y轴于E,过A作AF⊥DE于F,则△ABD为等腰直角三角形,易得△AFD≌△DEB,依据全等三角形的性质,即可得出D(![]() ,
,![]() ),进而得出直线AD的解析式,解方程组即可得到C点坐标.
),进而得出直线AD的解析式,解方程组即可得到C点坐标.
解:如图所示,过B作BD⊥AC于D,过D作DE⊥y轴于E,过A作AF⊥DE于F,
∵AB绕点A逆时针旋转45°,BD⊥AC
∴∠DAB=∠DBA=45°
∴AD=BD,即△ABD为等腰直角三角形
又∵BD⊥AC,过D作DE⊥y轴于E,过A作AF⊥DE于F
∴∠AFD=∠BED=90°,∠ADF+∠BDE=90°,∠ADF+∠FAD=90°
∴∠BDE=∠FAD
△AFD≌△DEB(AAS),
设DF=BE=a,
∵B(0,2),A(﹣6,﹣1),
∴OE=a+2=GF,DE=6﹣a,AF=a+3,
∵AF=DE,
∴a+3=6﹣a,
解得a=![]() ,
,
∴D(![]() ,
,![]() ),
),
设直线AD的解析式为y=k'x+b,则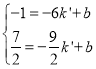 ,
,
解得![]() ,
,
∴y=3x+17,
∵A(﹣6,﹣1)在反比例函数![]() 的图象上,
的图象上,
∴k=6,即y=![]() ,
,
解方程组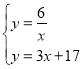 ,可得
,可得![]() 或
或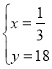 ,
,
∴点C的坐标为(![]() ,18),
,18),
故答案为:(![]() ,18).
,18).


科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用 (元) | ||
A | B | ||
第一次 | 20 | 50 | 4100 |
第二次 | 30 | 40 | 3700 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件50元出售,
商品以每件50元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的
商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
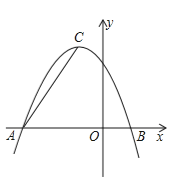
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别是
轴的两个交点分别是![]() 、
、![]() ,
,![]() 为顶点.
为顶点.
(1)求![]() 、
、![]() 的值和顶点
的值和顶点![]() 的坐标;
的坐标;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为斜边的直角三角形?若存在,求出点
为斜边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千 克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)(3分)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)(3分)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)(4分)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初期,天气炎热,水杯需求量大.双福育才中学门口某超市购进一批水杯,其中A种水杯进价为每个15元,售价为每个25元;B种水杯进价为每个12元,售价为每个20元
(1)该超市平均每天可售出60个A种水杯,后来经过市场调查发现,A种水杯单价每降低1元,则平均每天的销量可增加10个.为了尽量让学生得到更多的优惠,某天该超市将A种水杯售价调整为每个m元,结果当天销售A种水杯获利630元,求m的值.
(2)该超市准备花费不超过1600元的资金,购进A、B两种水杯共120个,其中B种水杯的数量不多于A种水杯数量的两倍.请为该超市设计获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
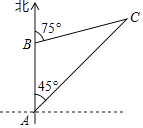
【题目】一艘货轮以34海里/时的速度在海面上向正南方向航行,当它行驶至B处时,某观察者发现在货轮的北偏东75°方向有一灯塔C;货轮继续向南航行1.5小时后到达A处,某观察者再次发现灯塔C在货轮的东北方向.求此时货轮与灯塔C的距离.(结果保留到个位)(参考数据:sin75°≈0.97,cos75°≈0.29,tan75°≈3.73,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com