
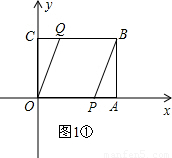
 解:(1)①四边形OPBQ是平行四边形,理由如下:
解:(1)①四边形OPBQ是平行四边形,理由如下: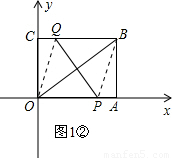 ②设经过t秒能够使得QP⊥OB.
②设经过t秒能够使得QP⊥OB. .
. 秒能够使得QP⊥OB;
秒能够使得QP⊥OB;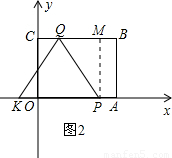 (2)设经过t秒,△PQK是等边三角形.
(2)设经过t秒,△PQK是等边三角形.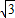 .
.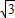 时,∵AK=AP+PK=AP+PQ=t+16-4t=16-3t=16-3(4-
时,∵AK=AP+PK=AP+PQ=t+16-4t=16-3t=16-3(4-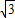 )=4+3
)=4+3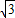 >8,
>8,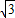 -8=3
-8=3 -4,
-4,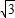 ,0),运动时间(4-
,0),运动时间(4-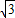 )秒;
)秒; 时,∵OK=OP+PK=AP+PQ=8-t+16-4t=24-5t=24-5(4+
时,∵OK=OP+PK=AP+PQ=8-t+16-4t=24-5t=24-5(4+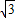 )=4-5
)=4-5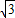 <0,
<0,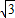 不合题意舍去.
不合题意舍去.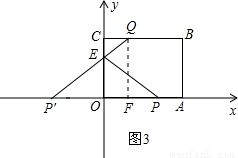 故点K在x轴上,经过(4-
故点K在x轴上,经过(4- )秒时,△PQK是等边三角形,此时点K的坐标为(4-3
)秒时,△PQK是等边三角形,此时点K的坐标为(4-3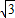 ,0);
,0);

科目:初中数学 来源: 题型:
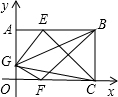 如图,已知OABC是一个长方形,其中顶点A,B的坐标分别为(0,a)和(9,a),点E在AB上,且AE=AG,点F在OC上,且OF=
如图,已知OABC是一个长方形,其中顶点A,B的坐标分别为(0,a)和(9,a),点E在AB上,且AE=AG,点F在OC上,且OF=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
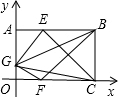 如图,已知OABC是一个长方形,其中顶点A,B的坐标分别为(0,a)和(9,a),点E在AB上,且AE=AG,点F在OC上,且OF=
如图,已知OABC是一个长方形,其中顶点A,B的坐标分别为(0,a)和(9,a),点E在AB上,且AE=AG,点F在OC上,且OF= OC,点G在OA上,且使△GEC的面积为20,△GFB的面积为16,试求a的值.
OC,点G在OA上,且使△GEC的面积为20,△GFB的面积为16,试求a的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com