练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知OB＝OC，∠A＝∠D，求证：∠ABC＝∠DCB.

    先由OB＝OC，∠A＝∠D，结合对顶角相等根据“AAS”证得△AOB≌△DOC，即可得到∠OBA＝∠OCD，再由OB=OC根据等边对等角得到∠OBC＝∠OCB，即可证得结论.

    解析试题分析：在△AOB和△DOC中
    ∠AOB＝∠DOC
    ∠A＝∠D
    OB＝OC
    ∴△AOB≌△DOC（AAS）
    ∴∠OBA＝∠OCD
    ∵OB=OC
    ∴∠OBC＝∠OCB
    ∴∠OBA+∠OBC＝∠OCB+∠OCD
    ∴∠ABC＝∠DCB.
    考点：本题考查的是全等三角形的判定和性质
    点评：解答本题的关键是熟练掌握全等三角形的对应角相等，注意对应字母要写在对应位置上.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：学习周报　数学　沪科八年级版　2009－2010学年　第12期　总168期 沪科版 题型：013

    如图，已知OA＝OB，OC＝OD，∠O＝50°，∠D＝35°，则∠AEC等于

    [　　]

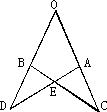
    A．60°

    B．50°

    C．45°

    D．30°

    查看答案和解析>>

    科目：初中数学 来源：中学教材全解　七年级数学上　（北师大版） 北师大版 题型：044

    如图，已知OB、OC是∠AOD内部的两条射线，OM平分∠AOB、ON平分∠COD，若∠AOD＝α，∠MON＝β求∠BOC的大小(用含α、β的式子表示)．

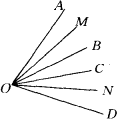
    查看答案和解析>>

    科目：初中数学 来源：精编教材全解·数学(七年级上册)　苏科版 苏科版 题型：013

    如图，已知∠AOC＝α，OA⊥OB，OD⊥OC，垂足均为O，则∠BOD的度数是(　　)．

    [　　]

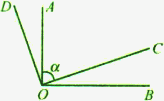
    A．180°－α

    B．90°－α

    C．90°＋α

    D．2α－90°

    查看答案和解析>>

    科目：初中数学 来源：2012-2013年云南西佤族自治县一中八年级上期末考试数学试卷（解析版） 题型：解答题

    如图，已知OB＝OC，∠A＝∠D，求证：∠ABC＝∠DCB.

     

    查看答案和解析>>

    同步练习册答案