Question

18．设点P为抛物线y=（x+2）²上的任意一点，将整条抛物线绕其顶点G顺时针方向旋转90°后得到一个新图形（仍为抛物线），点P在新图形中的对应点记为Q．
（1）当点P的横坐标为-4时，求点Q的坐标．
（2）设Q（m，n），试用n表示m．

Answer 1

分析 （1）首先根据m的值确定出原抛物线的解析式，进而可求得P、G的坐标，过P作PE⊥x轴于E，过Q作QF⊥x轴于F，根据旋转的性质知：△GQF≌△PGE，则QF=GE、PE=GF，可据此求得点Q的坐标．
（2）已知Q点坐标，即可得到QF、FG的长，仿照（1）的方法可求出点P的坐标，然后代入原抛物线的解析式中，可求得a、b、m的关系式．

解答 解：（1）y=（x+2）²，
则G（-2，0），
∵点P的横坐标为4，且P在抛物线上，
∴将x=-4代入抛物线解析式得：y=（-4+2）²=4，
∴P（-4，4），
如图，连接QG、PG，过点Q作QF⊥x轴于F，过点P作PE⊥x轴于E，
依题意，可得△GQF≌△PGE；
则FQ=EG=2，FG=EP=4，
∴FO=2．
∴Q（2，2）．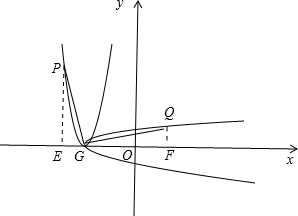


（2）已知Q（m，n），则GE=QF=n，FG=m+2；
由（1）知：PE=FG=m+2，GE=QF=n，即P（-2-n，m+2），
代入原抛物线的解析式中，得：m+2=（-2-n+2）²，
m=n²-2，

点评 此题主要考查了图形的旋转变换、全等三角形的判定和性质、函数图象上点的坐标意义等知识，难度较大．