
【题目】如图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径是6cm,下底面直径为4cm,母线长为EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积(面积计算结果用![]() 表示) .
表示) .
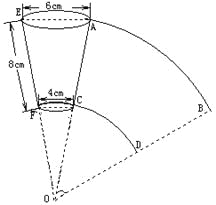
【答案】扇形OAB的圆心角为45°,纸杯的表面积为44![]() .
.
【解析】
试题设扇形OAB的圆心角为n°,然后根据弧长AB等于纸杯上开口圆周长和弧长CD等于纸杯下底面圆周长,列关于n和OF的方程组,解方程组可得出n和OF的值,然后根据纸杯表面积=纸杯侧面积+纸杯底面积=扇形OAB的面积-扇形OCD的面积+纸杯底面积,计算即可.
试题解析: 设扇形OAB的圆心角为n°
弧长AB等于纸杯上开口圆周长:![]()
弧长CD等于纸杯下底面圆周长:![]()
可列方程组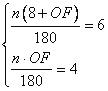 ,解得
,解得![]()
所以扇形OAB的圆心角为45°,OF等于16cm
纸杯表面积=纸杯侧面积+纸杯底面积=扇形OAB的面积-扇形OCD的面积+纸杯底面积即
S纸杯表面积
=![]()
=![]()


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
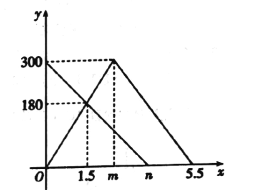
【题目】甲、乙两车分别从![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地立即以另一速度按原路匀速返回到
地立即以另一速度按原路匀速返回到![]() 地,乙车匀速前往
地,乙车匀速前往![]() 地.设甲、乙两车距
地.设甲、乙两车距![]() 地的路程为
地的路程为![]() (千米),甲车行驶的时间为
(千米),甲车行驶的时间为![]() (小时),
(小时),![]() 与
与![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)图中,![]() ,
,![]() ;
;
(2)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在甲车返回到![]() 地的过程中,当
地的过程中,当![]() 为何值时,甲、乙两车相距190千米?
为何值时,甲、乙两车相距190千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=![]() .
.
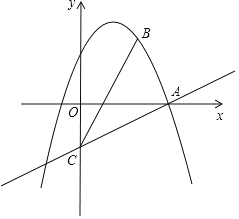
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
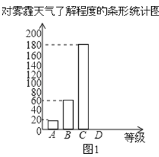
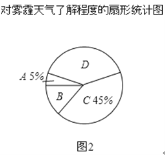
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=6,BC=8,点D、E分别在BC,AC上,且∠ADE=∠B,若△ADE是等腰三角形,则BD的长为_________.
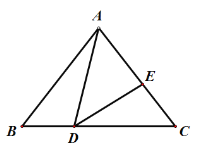
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com