【答案】
分析:(1)首先连接OE,由
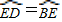
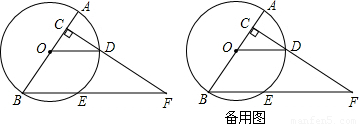
,OD∥BF,易得∠OBE=∠OEB=∠BOE=60°,又由CF⊥AB,即可求得∠F的度数;
(2)作OH⊥BE,垂足为H,易得△HBO≌△COD,即可得CO=BH=x,求得BE=2x,易得△COD∽△CBF,然后由相似三角形的对应边成比例,可得
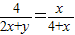
,则可求得y与x之间的函数解析式;
(3)由∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB,可得∠COD=∠DOE,即可得C关于直线OD的对称点为P在线段OE上,然后分别从PB=PE,EB=EP,BE=BP去分析求解即可求得答案.
解答:解:(1)连接OE,-------------------------------------------------------(1分)
∵
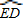
=
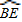
,
∴∠BOE=∠EOD-------------------------------------------------------------------(1分)
∵OD∥BF,
∴∠DOE=∠BEO,
∵OB=OE,
∴∠OBE=∠OEB,-------------------------------------------------------------------(1分)
∴∠OBE=∠OEB=∠BOE=60°,---------------------------------------------------------------------(1分)
∵CF⊥AB,
∴∠FCB=90°,
∴∠F=30°;--------------------------------------------------------------------------(1分)
(2)作OH⊥BE,垂足为H,-----------------------------------------------------------------------------(1分)
∵在△HBO和△COD中,
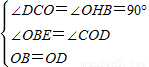
,
∴△HBO≌△COD(AAS),-------------------------------------------------------------------------------------(1分)
∴CO=BH=x,
∴BE=2x,
∵OD∥BF,
∴△COD∽△CBF,
∴
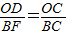
,--------------------------------------------------------------------(1分)
∴
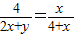
,
∴y=
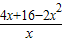
(0<x<4);-------------------------(2分)
(3)∵∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB,
∴∠COD=∠DOE,
∴C关于直线OD的对称点为P在线段OE上,----------------(1分)
若△PBE为等腰三角形,
设CO=x,
∴OP=OC=x,
则PE=OE-OP=4-x,
由(2)得:BE=2x,
①当PB=PE,不合题意舍去;--------------------------------------------------------------(1分)
②当EB=EP,2x=4-x,
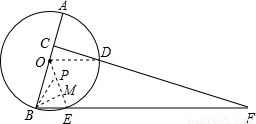
解得:x=

,---------------------------------------------------------(1分)
③当BE=BP,作BM⊥OE,垂足为M,
∴EM=

PE=
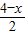
,
∴∠OEB=∠COD,∠BME=∠DCO=90°,
∴△BEM∽△DOC,
∴
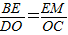
,
∴
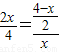
,
整理得:x
2+x-4=0,
解得:x=
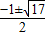
(负数舍去).----------------------------------(1分)
综上所述:当OC的长为

或
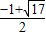
时,△PBE为等腰三角形.
点评:此题考查了圆的性质、等边三角形的判定与性质、等腰三角形的性质、全等三角形的判定与性质以及相似三角形的判定与性质等性质.此题综合性较强,难度较大,注意掌握辅助线的作法,注意数形结合思想、分类讨论思想与方程思想的应用.

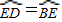 ,求∠F的度数;
,求∠F的度数;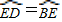 ,OD∥BF,易得∠OBE=∠OEB=∠BOE=60°,又由CF⊥AB,即可求得∠F的度数;
,OD∥BF,易得∠OBE=∠OEB=∠BOE=60°,又由CF⊥AB,即可求得∠F的度数;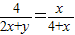 ,则可求得y与x之间的函数解析式;
,则可求得y与x之间的函数解析式;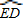 =
=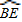 ,
, (2)作OH⊥BE,垂足为H,-----------------------------------------------------------------------------(1分)
(2)作OH⊥BE,垂足为H,-----------------------------------------------------------------------------(1分)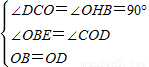 ,
,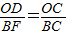 ,--------------------------------------------------------------------(1分)
,--------------------------------------------------------------------(1分)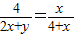 ,
,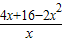 (0<x<4);-------------------------(2分)
(0<x<4);-------------------------(2分)
 ,---------------------------------------------------------(1分)
,---------------------------------------------------------(1分) PE=
PE=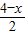 ,
,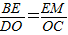 ,
,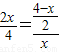 ,
,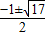 (负数舍去).----------------------------------(1分)
(负数舍去).----------------------------------(1分) 或
或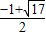 时,△PBE为等腰三角形.
时,△PBE为等腰三角形.

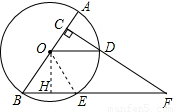
 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.