
”¾ĢāÄæ”æŅŃÖŖ![]() ŹĒ×ī“óµÄøŗÕūŹż£¬
ŹĒ×ī“óµÄøŗÕūŹż£¬![]() £¬CŹĒ-4µÄĻą·“Źż£¬ĒŅ
£¬CŹĒ-4µÄĻą·“Źż£¬ĒŅ![]() ”¢
Ӣ![]() Ӣ
”¢![]() ·Ö±šŹĒµć
·Ö±šŹĒµć![]() ”¢
Ӣ![]() Ӣ
”¢![]() ŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹż£®
ŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹż£®
![]()
£Ø1£©Ēó![]() ”¢
Ӣ![]() Ӣ
”¢![]() µÄÖµ£¬²¢ŌŚŹżÖįÉĻ±ź³öµć
µÄÖµ£¬²¢ŌŚŹżÖįÉĻ±ź³öµć![]() ”¢
Ӣ![]() Ӣ
”¢![]() £®
£®
£Ø2£©ŌŚŹżÖįÉĻ£¬Čō![]() µ½
µ½![]() µÄ¾ąĄėøÕŗĆŹĒ3£¬Ōņ
µÄ¾ąĄėøÕŗĆŹĒ3£¬Ōņ![]() µć½Š×ö
µć½Š×ö![]() µÄ”°ŠŅø£µć”±Ōņ
µÄ”°ŠŅø£µć”±Ōņ![]() µÄŠŅø£µć
µÄŠŅø£µć![]() Ėł±ķŹ¾µÄŹżÓ¦øĆŹĒ_________£®
Ėł±ķŹ¾µÄŹżÓ¦øĆŹĒ_________£®
£Ø3£©Čō¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢ŃŲŹżÖįĻņÕż·½ĻņŌĖ¶Æ£¬¶Æµć
³ö·¢ŃŲŹżÖįĻņÕż·½ĻņŌĖ¶Æ£¬¶Æµć![]() Ķ¬Ź±“Óµć
Ķ¬Ź±“Óµć![]() ³ö·¢Ņ²ŃŲŹżÖįĻņÕż·½ĻņŌĖ¶Æ£¬µć
³ö·¢Ņ²ŃŲŹżÖįĻņÕż·½ĻņŌĖ¶Æ£¬µć![]() µÄĖŁ¶ČŹĒĆæĆė3øöµ„Ī»³¤¶Č£¬µć
µÄĖŁ¶ČŹĒĆæĆė3øöµ„Ī»³¤¶Č£¬µć![]() µÄĖŁ¶ČŹĒĆæĆė1øöµ„Ī»³¤¶Č£¬ĒóŌĖ¶Æ¼øĆėŗ󣬵ć
µÄĖŁ¶ČŹĒĆæĆė1øöµ„Ī»³¤¶Č£¬ĒóŌĖ¶Æ¼øĆėŗ󣬵ć![]() æÉŅŌ×·ÉĻµć
æÉŅŌ×·ÉĻµć![]() £®
£®
£Ø4£©ŌŚŹżÖįÉĻ£¬Čō![]() µ½
µ½![]() ”¢
”¢![]() µÄ¾ąĄėÖ®ŗĶĪŖ6£¬Ōņ
µÄ¾ąĄėÖ®ŗĶĪŖ6£¬Ōņ![]() ½Š×ö
½Š×ö![]() ”¢
”¢![]() µÄŠŅø£ÖŠŠÄ”±ĒėÖ±½ÓŠ“³öĖłÓŠµć
µÄŠŅø£ÖŠŠÄ”±ĒėÖ±½ÓŠ“³öĖłÓŠµć![]() ŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹż£®
ŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹż£®
”¾“š°ø”æ£Ø1£©a=-1£¬b=-5£¬c=4£»£Ø2£©£4»ņ2£»£Ø3£©t=2£»£Ø4£©![]() »ņ
»ņ![]()
”¾½āĪö”æ
£Ø1£©Ąķ½āÓėÕūŹż”¢Ļą·“Źż”¢¾ų¶ŌÖµÓŠ¹ŲøÅÄī£¬Äܹ»ÕżČ·»³öŹżÖį£¬ÕżČ·ŌŚŹżÖįÉĻÕŅµ½Ėł¶ŌÓ¦µÄµć£»
£Ø2£©øł¾Ż”°![]() µ½
µ½![]() µÄ¾ąĄėøÕŗĆŹĒ3”±ÓŠĮ½µć£¬ĄūÓĆĮ½µć¼ä¾ąĄė¹«Ź½Ēó½ā¼“æÉ.
µÄ¾ąĄėøÕŗĆŹĒ3”±ÓŠĮ½µć£¬ĄūÓĆĮ½µć¼ä¾ąĄė¹«Ź½Ēó½ā¼“æÉ.
£Ø3£©øł¾ŻŹżÖįÉĻĮ½µć¼äµÄ¾ąĄėĮŠ³ö·½³Ģ½ųŠŠĒó½ā¼“æÉ£»
£Ø4£©×¢ŅāŹżÖįÉĻĮ½µć¼äµÄ¾ąĄė¹«Ź½£ŗĮ½µćĖł¶ŌÓ¦µÄŹżµÄ²īµÄ¾ų¶ŌÖµ£®
£Ø1£©![]() ŹĒ×ī“óµÄøŗÕūŹż£¬¼“
ŹĒ×ī“óµÄøŗÕūŹż£¬¼“![]() ŹĒŅ»4µÄĻą·“Źż£¬¼“
ŹĒŅ»4µÄĻą·“Źż£¬¼“![]() £¬
£¬
ĖłŅŌµć![]() ”¢
Ӣ![]() Ӣ
”¢![]() ŌŚŹżÖįÉĻĪ»ÖĆČēĶ¼ĖłŹ¾£ŗ
ŌŚŹżÖįÉĻĪ»ÖĆČēĶ¼ĖłŹ¾£ŗ
![]()
£Ø2£©µ±DŌŚAµć×ó²ąŹ±£¬Dµć¶ŌÓ¦µÄŹżĪŖ£ŗ-1-3=-4£»
µ±DŌŚAµćÓŅ²ąŹ±£¬Dµć¶ŌÓ¦µÄŹżĪŖ£ŗ-1+3=2£»
¹Ź“š°øĪŖ£ŗ-4»ņ2£»
£Ø3£©ÉčŌĖ¶Æ![]() Ćėŗ󣬵ć
Ćėŗ󣬵ć![]() æÉŅŌ×·ÉĻµć
æÉŅŌ×·ÉĻµć![]() Ōņµć
Ōņµć![]() ±ķŹ¾Źż
±ķŹ¾Źż![]() £¬µć
£¬µć![]() ±ķŹ¾
±ķŹ¾![]() £¬
£¬
ŅĄĢāŅāµĆ![]() £¬
£¬
½āµĆ£ŗ![]() £®
£®
“š£ŗŌĖ¶Æ2Ćėŗ󣬵ć![]() æÉŅŌ×·ÉĻµć
æÉŅŌ×·ÉĻµć![]() £»
£»
£Ø4£©“ęŌŚµćM£¬Ź¹Mµ½A”¢CĮ½µćµÄ¾ąĄėÖ®ŗĶµČÓŚ6£¬
”ß|AC|=|-1-4|=5<6£¬
”ąµćMŌŚAµćµÄ×ó²ą»ņŌŚCµćµÄÓŅ²ą£¬ÉčµćM±ķŹ¾µÄŹżĪŖx£¬
µ±MŌŚAµć×ó²ąŹ±£¬ŌņÓŠ|x+1|+|x-4|=6£¬µ±x£¼-1Ź±£¬½āµĆx=![]() £»
£»
µ±MŌŚCµćÓŅ²ąŹ±£¬ŌņÓŠ|x+1|+|x-4|=6£¬µ±x£¾4Ź±£¬½āµĆx=![]() £®
£®
¹ŹŹ¹µćMµ½A”¢CĮ½µćµÄ¾ąĄėÖ®ŗĶµČÓŚ6£¬µćM¶ŌÓ¦µÄŹżŹĒ![]() »ņ
»ņ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÖ±ĻßAB”ĪCD£¬Ö±ĻßEF·Ö±š½»AB”¢CDÓŚA”¢C£¬CMŹĒ”ĻACDµÄĘ½·ÖĻߣ¬CM½»ABÓŚH£¬¹żA×÷AG”ĶAC½»CMÓŚG£®
£Ø1£©ČēĶ¼1£¬µćGŌŚCHµÄŃÓ³¤ĻßÉĻŹ±£¬
¢ŁČō”ĻGAB=36”ć£¬Ōņ”ĻMCD=______£®
¢Ś²ĀĻė£ŗ”ĻGABÓė”ĻMCDÖ®¼äµÄŹżĮæ¹ŲĻµŹĒ______£®
£Ø2£©ČēĶ¼2£¬µćGŌŚCHÉĻŹ±£¬£Ø1£©¢Ś²ĀĻėµÄ”ĻGABÓė”ĻMCDÖ®¼äµÄŹżĮæ¹ŲĻµ»¹³ÉĮ¢Āš£æČē¹ū³ÉĮ¢£¬Ēėøų³öÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėŠ“³ö”ĻGABÓė”ĻMCDÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
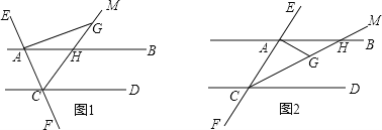
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»¼ÜŌĘĢŻ³¤25 m£¬Š±ææŌŚŅ»ĆęĒ½ÉĻ£¬ĢŻ×ÓææĒ½µÄŅ»¶Ė¾ąµŲĆę24 m.
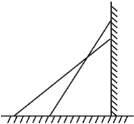
(1)ÕāøöĢŻ×ӵ׶ĖĄėĒ½ÓŠ¶ąÉŁĆ×£æ
(2) Čē¹ūĢŻ×ӵĶ„¶ĖĻĀ»¬ĮĖ4m£¬ÄĒĆ“ĢŻ×ӵĵײæŌŚĖ®Ę½·½ĻņŅ²»¬¶ÆĮĖ4mĀš?ĪŖŹ²Ć“?
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷ABCµÄÖܳ¤ŹĒ21£¬BO”¢CO·Ö±šĘ½·Ö”ĻABCŗĶ”ĻACB£¬OD”ĶBCÓŚD£¬OE”ĶAB£¬OF”ĶAC£¬ĒŅOD=3£®
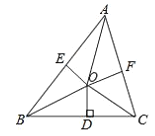
£Ø1£©ŹŌÅŠ¶ĻĻ߶ĪOD”¢OE”¢OFµÄ“󊔹ŲĻµ£®
£Ø2£©Ēó”÷ABCµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µČ±ß”÷ABCŗĶµČ±ß”÷ECDµÄ±ß³¤ĻąµČ£¬BCÓėCDĮ½±ßŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬Ēėøł¾ŻČēĻĀŅŖĒó£¬Ź¹ÓĆĪŽæĢ¶ČµÄÖ±³ß£¬ĶعżĮ¬Ļߵķ½Ź½»Ķ¼£®
(1)ŌŚĶ¼1ÖŠ»Ņ»øöÖ±½ĒČż½ĒŠĪ£» (2)ŌŚĶ¼2ÖŠ»³ö”ĻACEµÄĘ½·ÖĻߣ®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
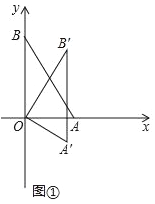
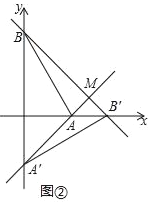
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬OĪŖŌµć£¬µćA£Ø1£¬0£©£¬µćB£Ø0£¬ ![]() £©£¬°Ń”÷ABOČʵćOĖ³Ź±ÕėŠż×Ŗ£¬µĆA”äB”äO£¬¼ĒŠż×Ŗ½ĒĪŖ¦Į£®
£©£¬°Ń”÷ABOČʵćOĖ³Ź±ÕėŠż×Ŗ£¬µĆA”äB”äO£¬¼ĒŠż×Ŗ½ĒĪŖ¦Į£®
£Ø¢ń£©ČēĶ¼¢Ł£¬µ±¦Į=30”揱£¬ĒóµćB”äµÄ×ų±ź£»
£Ø¢ņ£©ÉčÖ±ĻßAA”äÓėÖ±ĻßBB”äĻą½»ÓŚµćM£®
ČēĶ¼¢Ś£¬µ±¦Į=90”揱£¬ĒóµćMµÄ×ų±ź£»
¢ŚµćC£Ø©1£¬0£©£¬ĒóĻ߶ĪCM³¤¶ČµÄ×īŠ”Öµ£®£ØÖ±½ÓŠ“³ö½į¹ū¼“æÉ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćBŌŚĻ߶ĪACÉĻ£¬µćEŌŚĻ߶ĪBDÉĻ£¬”ĻABD=”ĻDBC£¬AB=DB£¬EB=CB£¬M£¬N·Ö±šŹĒAE£¬CDµÄÖŠµć”£ŹŌĢ½Ė÷BMŗĶBNµÄ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ”£

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻBAC=90”ć£¬AC=2AB£¬µćDŹĒACµÄÖŠµć£®½«Ņ»æéČń½ĒĪŖ45”ćµÄÖ±½ĒČż½Ē°åČēĶ¼·ÅÖĆ£¬Ź¹Čż½Ē°åŠ±±ßµÄĮ½øö¶Ėµć·Ö±šÓėA”¢DÖŲŗĻ£¬Į¬½ÓBE”¢EC£®
 ŹŌ²ĀĻėĻ߶ĪBEŗĶECµÄŹżĮæ¼°Ī»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®
ŹŌ²ĀĻėĻ߶ĪBEŗĶECµÄŹżĮæ¼°Ī»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼£Ø1£©£¬ŅŃÖŖ£ŗŌŚ”÷ABCÖŠ£¬”ĻBAC£½90”ć£¬AB=AC£¬Ö±Ļßm¾¹żµćA£¬BD”ĶÖ±Ļßm, CE”ĶÖ±Ļßm,“¹×ć·Ö±šĪŖµćD”¢E.Ö¤Ć÷:DE=BD+CE.
£Ø2£© ČēĶ¼£Ø2£©£¬½«£Ø1£©ÖŠµÄĢõ¼žøÄĪŖ£ŗŌŚ”÷ABCÖŠ£¬AB=AC£¬D”¢A”¢EČżµć¶¼ŌŚÖ±ĻßmÉĻ,²¢ĒŅÓŠ”ĻBDA=”ĻAEC=”ĻBAC=![]() ,ĘäÖŠ
,ĘäÖŠ![]() ĪŖČĪŅāČń½Ē»ņ¶Ū½Ē.ĒėĪŹ½įĀŪDE=BD+CEŹĒ·ń³ÉĮ¢?Čē³ÉĮ¢,ĒėÄćøų³öÖ¤Ć÷;Čō²»³ÉĮ¢,ĒėĖµĆ÷ĄķÓÉ.
ĪŖČĪŅāČń½Ē»ņ¶Ū½Ē.ĒėĪŹ½įĀŪDE=BD+CEŹĒ·ń³ÉĮ¢?Čē³ÉĮ¢,ĒėÄćøų³öÖ¤Ć÷;Čō²»³ÉĮ¢,ĒėĖµĆ÷ĄķÓÉ.
£Ø3£©ĶŲÕ¹ÓėÓ¦ÓĆ£ŗČēĶ¼£Ø3£©£¬D”¢EŹĒD”¢A”¢EČżµćĖłŌŚÖ±ĻßmÉĻµÄĮ½¶Æµć£ØD”¢A”¢EČżµć»„²»ÖŲŗĻ£©,µćFĪŖ”ĻBACĘ½·ÖĻßÉĻµÄŅ»µć,ĒŅ”÷ABFŗĶ”÷ACF¾łĪŖµČ±ßČż½ĒŠĪ£¬Į¬½ÓBD”¢CE,Čō”ĻBDA=”ĻAEC=”ĻBAC£¬ŹŌÅŠ¶Ļ”÷DEFµÄŠĪד.

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com