
【题目】已知关于x的一元二次方程![]() 。
。
(1)如果方程根的判别式的值为1,求m的值。
(2)如果方程有一个根是—1,求此方程的根的判别式的值。
科目:初中数学 来源: 题型:
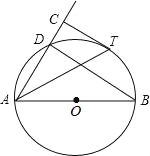
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过![]() 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=![]() (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(1)求点D的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,网格图由边长为1的小正方形所构成,Rt△ABC的顶点分别是A(-1,3),B(-3,-1),C(-3,3).

(1)请在图1中作出△ABC关于点(-1,0)成中心对称△![]() ,并分别写出A,C对应点的坐标
,并分别写出A,C对应点的坐标![]() ;
;![]()
(2)设线段AB所在直线的函数表达式为![]() ,试写出不等式
,试写出不等式![]() 的解集是 ;
的解集是 ;
(3)点M和点N 分别是直线AB和y轴上的动点,若以![]() ,
,![]() ,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
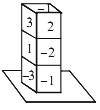
【题目】如图,将3个同样的正方体重叠放置在桌面上,每个正方体的6个面上分别写有-3、-2、-1、1、2、3,相对的两面上写的数字互为相反数,现在有5个面的数字无论从哪个角度都看不到,这5个看不到的面上数字的乘积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
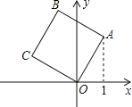
【题目】如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
A. (﹣2,1)B. (﹣1,2)C. (![]() ,﹣1)D. (﹣
,﹣1)D. (﹣![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
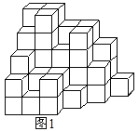
【题目】如图1,是一个由53个大小相同的小正方体堆成的立体图形,从正面观察这个立体图形得到的平面图形如图2所示.
(1)请在图3、图4中依次画出从左面、上面观察这个立体图形得到的平面图形
(2)保持这个立体图形中最底层的小正方体不动,从其余部分中取走k个小正方体,得到一个新的立体图形.如果依次从正面、左面、上面观察新的立体图形,所得到的平面图形分别与图2、图3、图4是一样的,那么k的最大值为 .



查看答案和解析>>
科目:初中数学 来源: 题型:
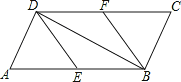
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的对角线相交于点
的对角线相交于点![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若将题设中“矩形![]() ”这一条件改为“菱形
”这一条件改为“菱形![]() ”,其余条件不变,则四边形
”,其余条件不变,则四边形![]() 是__________形.
是__________形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com