练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    想一想，如何把图（1）变化得到图（2）如果AD∥BC，AD=BC，AE=CF，能判断△ADF与△CBE全等吗？请你说出下面思考过程中每一步的理由精英家教网．
    因为AD∥BC，
    所以∠A=∠C，这是根据
     
    ．
    因为AE=CF，
    所以AF=CE，这是根据
     
    ．
    AD=CB
    ∠A=∠C
    AF=CE
    ?△ADF≌△CBE，这是根据
     
    ．
    分析：显然∠A、∠C是内错角，则依据是两直线平行内错角相等，第二个是等式的性质，两边夹一角是SAS．
    解答：解：（1）图（1）与图（2）比较可发现，将△ADC沿直线CA方向平移CF的长度即可得到图；
    （2）∵AD∥BC，
    ∴∠A=∠C，
    ∵AE=CF，
    ∴AF=CE，
    AD=CB
    ∠A=∠C
    AF=CE

    ∴△ADF≌△CBE．
    点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网有一位老人担心自己百年以后，两个儿子为争夺遗产而不和．想着如何把自己的家业分给两个儿子，其中有一块地是平行四边形，地里有一口井，井的位置不在地的中间（如图）．老人想井不能分，两人可共用，但地要平分，老人想了很长时间，终于找到了分地方案．请你想一想老人的分地方案可能是怎样的（画在图上）？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如何求22.5°的正切值，小明想了一个办法：把一张正方形纸片（正方形ABCD）按如图方式折叠，使顶点B恰好落在对角线AC上，折痕为EC．根据小明的操作通过计算可以得到tan22.5°=
    		2
    -1
    		2
    -1
    ．（保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在一次数学探究活动中，小强用一条直线把平行四边形ABCD分割成面积相等的两个部分．

    （1）根据小强的分割方法，你认为把平行四边形分割成面积相等的两个部分的直线有
    无数
    无数
     条．
    （2）请在图1中的三个平行四边形中分别画出满足小强分割方法的不同位置的一条直线．
    （3）由上述的思考，你能解决下面的问题吗？
    有一位老人担心自己百年以后，两个儿子为争夺遗产而不和，想着如何把自己的家业分给两个儿子，其中有一块地是平行四边形，地里有一口井，井的位置不在地的中间（如图2）．老人想：井不能分，两人共同使用，但地要分，老人想了很长时间，终于找到了分地方案．请你想一想老人分地方案可能是怎样的？（画在图上，并保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    想一想，如何把图（1）变化得到图（2）如果AD∥BC，AD=BC，AE=CF，能判断△ADF与△CBE全等吗？请你说出下面思考过程中每一步的理由．
    因为AD∥BC，
    所以∠A=∠C，这是根据______．
    因为AE=CF，
    所以AF=CE，这是根据______．
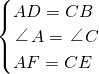    数学公式?△ADF≌△CBE，这是根据______．

    查看答案和解析>>

    同步练习册答案