
如图所示,P为矩形ABCD内一点,PA=3,PD=4,PC=5,求PB的长.

|
如图所示,将△ADP平移至△BCG,使A、D分别重合于B、C,连结PG交BC于O点.
∵AP ∴PG∥AB.又AB⊥BC,∴PG⊥BC. 在Rt△OPC中,PC2=OP2+OC2, 在Rt△OBG中,BG2=OG2+OB2, ∴PC2+BG2=OG2+OB2+OP2+OC2. 同理PB2+CG2=OG2+OB2+OP2+OC2. ∴PC2+BG2=PB2+CG2. 又PC=5,BG=PA=3,CG=PD=4, ∴PB2=PC2+BG2-CG2=32+52-42=18. ∴PB= 所以PB的长是 解析:已知条件PA、PC、PD的长和问题PB的长难以直接联系,同时又感觉到了3、4、5这一组数据非常好,不妨来考虑能否将它们放在同一个基本图形中. 说明:利用平移变换,将条件和问题有机结合,最终解决问题. |


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
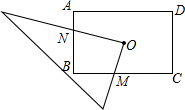 如图所示,O为矩形ABCD的对称中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=6,AD=8,OM=x,ON=y,则y与x的关系是
如图所示,O为矩形ABCD的对称中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=6,AD=8,OM=x,ON=y,则y与x的关系是| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,O为矩形ABCD的对称中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=6,AD=8,OM=x,ON=y,则y与x的关系是________(不填x的取值范围)
如图所示,O为矩形ABCD的对称中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=6,AD=8,OM=x,ON=y,则y与x的关系是________(不填x的取值范围)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
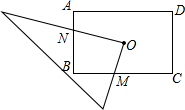
查看答案和解析>>
科目:初中数学 来源:2009年黑龙江省(鹤、伊、双、绥)升学大考数学试卷(五)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com