【题目】某市移动公司为了调查手机发送短信息的情况，在本区域的120位用户中抽取了10位用户来统计他们某周发信息的条数，结果如下表：
手机用户序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
发送短信息条数 | 20 | 19 | 20 | 20 | 21 | 17 | 15 | 23 | 20 | 25 |
本次调查中这120位用户大约每周一共发送条短信息．
灵星计算小达人系列答案科目：初中数学 来源： 题型：
【题目】花粉的质量很小，一粒某种植物花粉的质量约为0.000037 mg，已知1 g=1 000 mg，那么0.000 037 mg用科学记数法表示为（ ）
A. 3.7×10-5 g B. 3.7×10-6 g C. 3.7×10-7 g D. 3.7×10-8 g
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校有25名同学参加某比赛，预赛成绩各不相同，取前13名参加决赛，其中一名同学已经知道自己的成绩，能否进入决赛，只需要再知道这25名同学成绩的( )
A. 最高分 B. 平均数 C. 中位数 D. 方差
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），AB∥CD，猜想∠BPD与∠B、∠D的关系，说出理由．
解：猜想∠BPD+∠B+∠D=360°
理由：过点P作EF∥AB，
∴∠B+∠BPE=180°（两直线平行，同旁内角互补）
∵AB∥CD，EF∥AB，
∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）
∴∠EPD+∠D=180°（两直线平行，同旁内角互补）
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
（1）依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，并说明理由．
（2）观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，不需要说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】宏远商贸公司有A、B两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
体积（m3/件） | 质量（吨/件） | |
A型商品 | 0.8 | 0.5 |
B型商品 | 2 | 1 |
（1）已知一批商品有A、B两种型号，体积一共是20m3，质量一共是10.5吨，求A、B两种型号商品各有几件？
（2）物流公司现有可供使用的货车每辆额定载重3.5吨，容积为6m3，其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元．
要将（1）中的商品一次或分批运输到目的地，宏远商贸公司应如何选择运送、付费方式运费最少并求出该方式下的运费是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，矩形OABC的对角线AC=12，∠ACO=30°
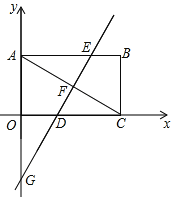
（1）求B、C两点的坐标；
（2）过点G（
）作GF⊥AC，垂足为F，直线GF分别交AB、OC于点E、D，求直线DE的解析式；
（3）在⑵的条件下，若点M在直线DE上，平面内是否存在点P，使以O、F、M、P为顶点的四边形是菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
