

分析 (1)因为∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形;
(2)因为PD∥BQ,当PD=BQ=BP时,四边形PBQD能成为菱形,先由PD=BQ求出运动时间t的值,再代入求BP,发现BP≠PD,判断此时四边形PBQD不能成为菱形;设Q点的速度改变为vcm/s时,四边形PBQD在时刻t为菱形,根据PD=BQ=BP列出关于v、t的方程组,解方程组即可求出点Q的速度.
解答 解:(1)∵∠B=90°,AP∥BQ,
∴当AP=BQ时,四边形ABQP成为矩形,
此时有t=22-3t,解得t=$\frac{11}{2}$.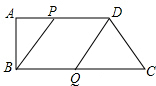
∴当t=$\frac{11}{2}$s时,四边形ABQP成为矩形;
(2)四边形PBQD不能成为菱形.理由如下:
∵PD∥BQ,
∴当PD=BQ=BP时,四边形PBQD能成为菱形.
由PD=BQ,得16-t=22-3t,解得t=3,
当t=3时,PD=BQ=13,BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{{8}^{2}+{t}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$≠13,
∴四边形PBQD不能成为菱形;
如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,
由题意,得$\left\{\begin{array}{l}{16-t=22-vt}\\{16-t=\sqrt{{8}^{2}+{t}^{2}}}\end{array}\right.$,解得 $\left\{\begin{array}{l}{t=6}\\{v=2}\end{array}\right.$.
故点Q的速度为2cm/s时,能够使四边形PBQD在某一时刻为菱形.
点评 本题借助动点主要考查了矩形、菱形的判定,勾股定理,等腰梯形的判定与性质,以及方程和方程组在几何图形中的应用,难度适中,用含t的代数式正确表示出相关线段的长度是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 该抛物线可由抛物线y=ax2向右平移2个单位,向下平移2个单位得到 | |
| B. | 若1<m<n<3,则a>0 | |
| C. | 若1<x0<3,则y0<0 | |
| D. | 不论a取何值,m+n=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
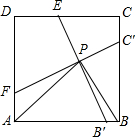 如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.
如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )| A. | 16$\sqrt{3}$ | B. | 32 | C. | 8$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$)-2=-9 | B. | $\sqrt{4}$=±2 | C. | -2(a-b)=-2a-2b | D. | ab4÷(-ab)=-b3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
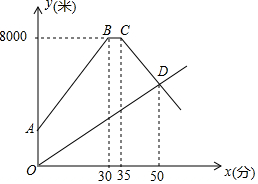 甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com