
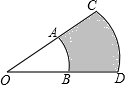
 如图,两个同心圆被两条半径截得的$\widehat{AB}$=6πcm,$\widehat{CD}$=10πcm,且AC=12cm,求阴影部分ABDC的面积.
如图,两个同心圆被两条半径截得的$\widehat{AB}$=6πcm,$\widehat{CD}$=10πcm,且AC=12cm,求阴影部分ABDC的面积. 分析 首先利用弧长公式求出n,x的值,再利用扇形面积公式求出部分圆环ABDC的面积.
解答 解:∵两个同心圆被两条半径截得$\widehat{AB}$的长为6πcm,$\widehat{CD}$的长为10πcm,又AC=12cm,
∴设AO=x,6π=$\frac{nπx}{180}$,
∴nx=1080,
10π=$\frac{nπ(12+x)}{180}$,
∴1800=12n+nx,
∴12n=720,
解得:n=60,
∴x=18,
则S扇形AOB=$\frac{1}{2}$×18×6π=54π,S扇形COD=$\frac{1}{2}$(18+12)×10π=150π,
∴部分圆环ABDC的面积为:S=150π-54π=96π.
点评 此题主要考查了扇形弧长公式以及扇形面积公式应用,根据已知得出扇形半径AO的长是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
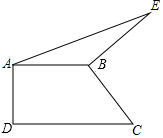 如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得到线段BE,连接AE.若AB=2,DC=4,则△ABE的面积为2.
如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得到线段BE,连接AE.若AB=2,DC=4,则△ABE的面积为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com