证明:在△ABC中,∠B=60°,
∴∠BAC+∠BCA=180°-∠B=180°-60°=120°.
∵AD平分∠BAC,CE平分∠ACB,
∴∠OAC=∠OAB=

∠BAC,∠OCD=∠OCA=

∠ACB,
在△OAC中,∠AOC=180°-(∠OAC+∠OCA)
=180°-

(∠BAC+∠ACB)=180°-

×120°=120°.
∴∠AOE=180°-∠AOC=180°-120°=60°.
在AC上截取AF=AE,连接OF,如图,
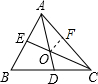
在△AOE和△AOF中,AE=AF,∠OAE=∠OAF,OA=OA,
∴△AOE≌△AOF(SAS),
∴∠AOE=∠AOF,
∴∠AOF=60°.
∴∠COF=∠AOC-∠AOF=120°-60°=60°.
又∠COD=60°,
∴∠COD=∠COF.
在△COD和△COF中,∠COD=∠COF,OC=OC,∠OCD=∠OCF,
∴△COD≌△COF(ASA),
∴CD=CF.
又∵AF=AE,
∴AC=AF+CF=AE+CD,
即AE+CD=AC.
分析:根据△ABC中,∠B=60°,所以∠BAC+∠BCA=120度.因为AD平分∠BAC,CE平分∠ACB,可求出∠AOC=120°,∠AOE=60度.在AC上截取AF=AE,连接OF,易证△AOE≌△AOF,∠AOE=∠AOF=60°,可证△COD≌△COF,则CD=CF.因为AF=AE,所以AC=AF+CF=AE+CD,即AE+CD=AC.
点评:本题考查了全等三角形的判定和性质;解答此题的关键是作出辅助线,构造全等三角形,把相关的线段划到同一个三角形中找关系.

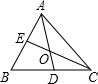 如图,在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O.试说明AE+CD=AC.
如图,在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O.试说明AE+CD=AC. ∠BAC,∠OCD=∠OCA=
∠BAC,∠OCD=∠OCA= ∠ACB,
∠ACB, (∠BAC+∠ACB)=180°-
(∠BAC+∠ACB)=180°- ×120°=120°.
×120°=120°.


 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为