
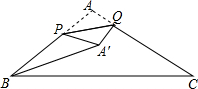
 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )| A. | 2$\sqrt{3}$-2 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 如图,当点Q与点C重合,A′点落在BC上时,BA′的长度最小,求出BA′即可解决问题.
解答 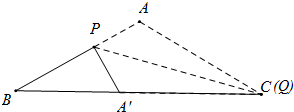 解:如图,当点Q与点C重合,A′点落在BC上时,BA′的长度最小.(圆外一点到圆上的点的最短的线段就是BA′,QA最长时,BA′最短)
解:如图,当点Q与点C重合,A′点落在BC上时,BA′的长度最小.(圆外一点到圆上的点的最短的线段就是BA′,QA最长时,BA′最短)
∵AB=AC=2,∠ABC=30°,
∴∠B=∠ACB=30°,∠BAC=180°-∠A-∠ACB=120°,
∵△PCA′是由△PCA翻折得到,
∴∠BAC=∠PA′C=120°,
∴∠PA′B=180°-∠PA′C=60°,
∴∠BPA′=90°,
∵BC=2$\sqrt{3}$,AC=A′C=2,
∴BA′=2$\sqrt{3}$-2,
∴BA′的最小值为2$\sqrt{3}$-2.
故选A.
点评 本题考查翻折变换、直角三角形30度角的性质、等腰三角形的性质等知识,利用特殊点是解决问题问题的关键,在最小值问题中属于比较难的题目.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
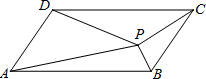 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )| A. | S1+S2=S3+S4 | B. | S1+S2>S3+S4 | C. | S1+S3=S2+S4 | D. | S1+S2<S3+S4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
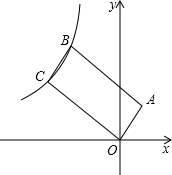 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
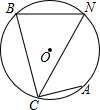 如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.
如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
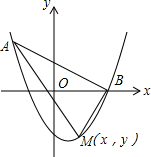 如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.
如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com