
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是__.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.

【答案】50°.
【解析】(1)根据等腰三角形的性质得出∠ABC=∠ACB=70°,求得∠A=40°,根据线段的垂直平分线的性质得出AN=BN,进而得出∠ABN=∠A=40°,根据三角形的内角和定理可得出∠ANB=100°,根据等腰三角形三线合一就可求得∠MNA=50°;
(2)①根据△NBC的周长=BN+CN+BC=AN+NC+BC就可求得.
②根据对称轴的性质,即可判定P就是N点,所以△PBC的周长最小值就是△NBC的周长.
解:(1)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠A=40°,
∵MN是AB的垂直平分线,
∴AN=BN,
∴∠ABN=∠A=40°,
∴∠ANB=100°,
∴∠MNA=50°;
故答案为50°.
(2)①∵AN=BN,
∴BN+CN=AN+CN=AC,
∵AB=AC=8cm,
∴BN+CN=8cm,
∵△NBC的周长是14cm.
∴BC=14﹣8=6cm.
②∵A、B关于直线MN对称,
∴连接AC与MN的交点即为所求的P点,此时P和N重合,
即△BNC的周长就是△PBC的周长最小值,
∴△PBC的周长最小值为14cm.


科目:初中数学 来源: 题型:
【题目】如图,某市有一块长为(3a+b) 米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=10,b=8,且每平方米造价为100元求出绿化需要多少费用.
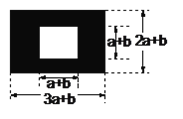
查看答案和解析>>
科目:初中数学 来源: 题型:
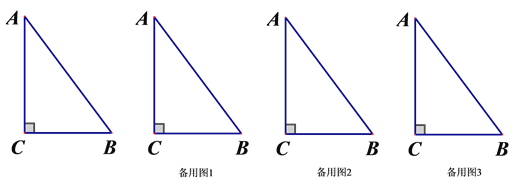
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C
的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)当t为几秒时,BP平分∠ABC
(3)问t为何值时,△BCP为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
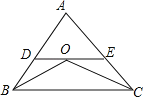
【题目】已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料(单位:毫米).

(1)此长方体包装盒的体积为______立方毫米(用含x,y的式子表示).
(2)若内部粘贴角料的面积占长方体表面纸板面积的![]() ,则当x=40,y=70时,制作这样一个长方体共需要纸板多少平方毫米?
,则当x=40,y=70时,制作这样一个长方体共需要纸板多少平方毫米?
查看答案和解析>>
科目:初中数学 来源: 题型:
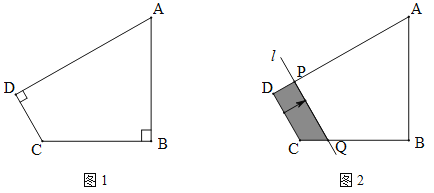
【题目】(2016四川省乐山市第23题)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=![]() .
.
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com